写在前面
最近刷LeetCode, 发现很多双百题解中用到的都是位运算技巧, 下面来总结一下位运算的常用技巧. 一开始参考了知乎的一篇回答, 里面推荐一本书叫做算法心得, 英文原版为Hackers Delight, 听这个名字就知道是一些hack技巧, 有机会一定要研读一下. 下面的代码用C++给出.
可能出现的一些数字:
- 48: ‘0’
- 65: ‘A’
- 97: ‘a’
预备知识
首先给出一些预备知识, 包括如何进制转换等.
任意进制到十进制
// 直观的想法
int x2dec_v1(string x, int k) {
int ans{}, n = x.size();
for (int i{}; i < n; ++i)
ans += (x[n - 1 - i] - '0') * pow(k, i); // with cmath
return ans;
}
// 或者更简洁的方法:
int x2dec_v2(string x, int k) {
int ans{};
for (char& c : x) ans = ans * k + (c - '0');
return ans;
}
十进制到任意进制
下面的都是针对$\leqslant10$进制而言的, 对于16进制, 需要特殊处理.
C++版本:
string dec2x(int x, int k) {
string ans{};
while (x) ans = to_string(x % k) + ans, x /= k;
return ans;
}
对于十六进制
405. 数字转换为十六进制数 - 力扣(LeetCode);
class Solution {
public:
string toHex(long num) {
string ans{};
if (num < 0) num += (1L << 32); // 负数的溢出表示
while (num) {
auto tmp{num % 16};
tmp += tmp > 9 ? 'a' - 10 : '0';
ans.push_back(tmp);
num /= 16;
}
reverse(ans.begin(), ans.end());
return ans.empty() ? "0"s : ans;
}
};
或者通过unsigned去掉负数的影响
class Solution {
public:
string toHex(unsigned num) {
string ans{};
while (num) {
auto tmp{num % 16};
tmp += tmp > 9 ? 'a' - 10 : '0';
ans.push_back(tmp);
num /= 16;
}
reverse(ans.begin(), ans.end());
return ans.empty() ? "0"s : ans;
}
};
分组位运算操作(二进制位的四个位成一组十六进制), 更加麻烦的位运算:
(值得学习, 因为没有更改形参类型)
class Solution {
public:
string toHex(int num) {
string ans{};
for (int i{7}; i >= 0; --i) {
int tmp{(num >> (i << 2)) & 0xf};
if (!ans.empty() || tmp)
ans.push_back(tmp > 9 ? tmp - 10 + 'a' : tmp + '0');
}
return ans.empty() ? "0"s : ans;
}
};
对于二进制
二进制的情况还有一种更优的方法, 如下: (其实思路还是分组)
string dec2bin(int x) {
string ans{};
for (int j = 31; j >= 0; --j) ans.push_back(x & (1 << j) ? '1' : '0');
return ans;
}
或者还有一种不显示前导零的方法:
string dec2bin_no_leading_zero(int x) {
string ans{};
for (int j = 31; j >= 0; --j) {
int tmp{x & (1 << j)};
if (!ans.empty() || tmp) ans.push_back(tmp ? '1' : '0');
}
return ans.empty() ? "0"s : ans;
}
对于26进制
class Solution {
public:
int titleToNumber(string columnTitle) {
int ans{};
for (int i{}; i < columnTitle.size(); ++i)
ans = ans * 26L + columnTitle[i] - 'A' + 1;
return ans;
}
};
168. Excel表列名称;(用例ZY直接杀我)
class Solution {
public:
string convertToTitle(int columnNumber) {
string ans{};
while (columnNumber) {
ans = static_cast<char>((columnNumber + 25L) % 26 + 'A') + ans;
columnNumber = (columnNumber - 1) / 26;
}
return ans;
}
};
对于负进制
class Solution {
public:
string baseNeg2(int n) {
string ans;
while (n) {
int res = n % -2; // 直接取余没问题
ans = to_string(abs(res)) + ans;
n = res < 0 ? n / (-2) + 1 : n / (-2); // 余数为负, 加一
}
return ans.empty() ? "0"s : ans;
}
};
class Solution {
public:
vector<int> addNegabinary(vector<int>& arr1, vector<int>& arr2) {
int i = arr1.size() - 1, j = arr2.size() - 1;
vector<int> ans;
for (int c{}; i >= 0 || j >= 0 || c; --i, --j) {
int a{i < 0 ? 0 : arr1[i]}, b{j < 0 ? 0 : arr2[j]};
int x{a + b + c};
c = 0;
if (x >= 2)
x -= 2, --c;
else if (x == -1)
x = 1, ++c;
ans.emplace_back(x);
}
// leading zero
while (ans.size() > 1 && ans.back() == 0) ans.pop_back();
reverse(ans.begin(), ans.end());
return ans;
}
};
负数的补码表示
为方便就用 python 了.
首先是从负十进制数到二进制的补码表示.
BIT_NUM = 32
def bitnot(num):
ans = ''
code = bin(-num)[2:]
# fill with zero
if (ln := len(code)) < BIT_NUM:
code = '0' * (BIT_NUM - ln) + code
for i in code:
ans += '1' if i == '0' else '0'
return ans
def get_complement_code(num):
if num >= 0:
return bin(num)[2:]
ccode = bin(int(bitnot(num), base=2) + 1)[2:]
# for pretty print, add ' ' every 8 bits
j = 0
for i in range(BIT_NUM):
if (i + 1) % 8 == 0:
ccode = ccode[:i+1+j] + ' ' + ccode[i+1+j:]
j += 1
return ccode
# usage:
print(get_complement_code(-72))
print(get_complement_code(-1))
'''
11111111 11111111 11111111 10111000
11111111 11111111 11111111 11111111
'''
然后是从补码表示得到十进制表示.
BIT_NUM = 8
def bitnot(num):
ans = ''
code = bin(-num)[2:]
# fill with zero
if (ln := len(code)) < BIT_NUM:
code = '0' * (BIT_NUM - ln) + code
for i in code:
ans += '1' if i == '0' else '0'
return ans
def get_num(s):
if s[0] == '0':
return int(s, base=2)
bn = bitnot(int(s, base=2) - 1)
return -int(bn, base=2)
print(get_num('10111000'))
print(get_num('11111111'))
'''
-72
-1
'''
下面就是正菜了:
位运算操作符
这里以C++为例.
有的语言可能有一些区别, 例如Java/JavaScript中的左移位还分为有符号(算术移位)和无符号(逻辑移位)的情况, 包括了三种移位操作.
| 运算名称 | 符号 | 运算规则 |
|---|---|---|
| 与 | & |
0&0=0 0&1=0 1&0=0 1&1=1 |
| 或 | | |
0|0=0 0|1=1 1|0=1 1|1=1 |
| 非 | ~ |
~0=1 ~1=0 |
| 异或 | ^ |
0^0=0 0^1=1 1^0=1 1^1=0 |
| 左移位 | << |
0001<<1 = 0010 |
| 右移位 | >> |
1000>>1 = 0100 |
优先级
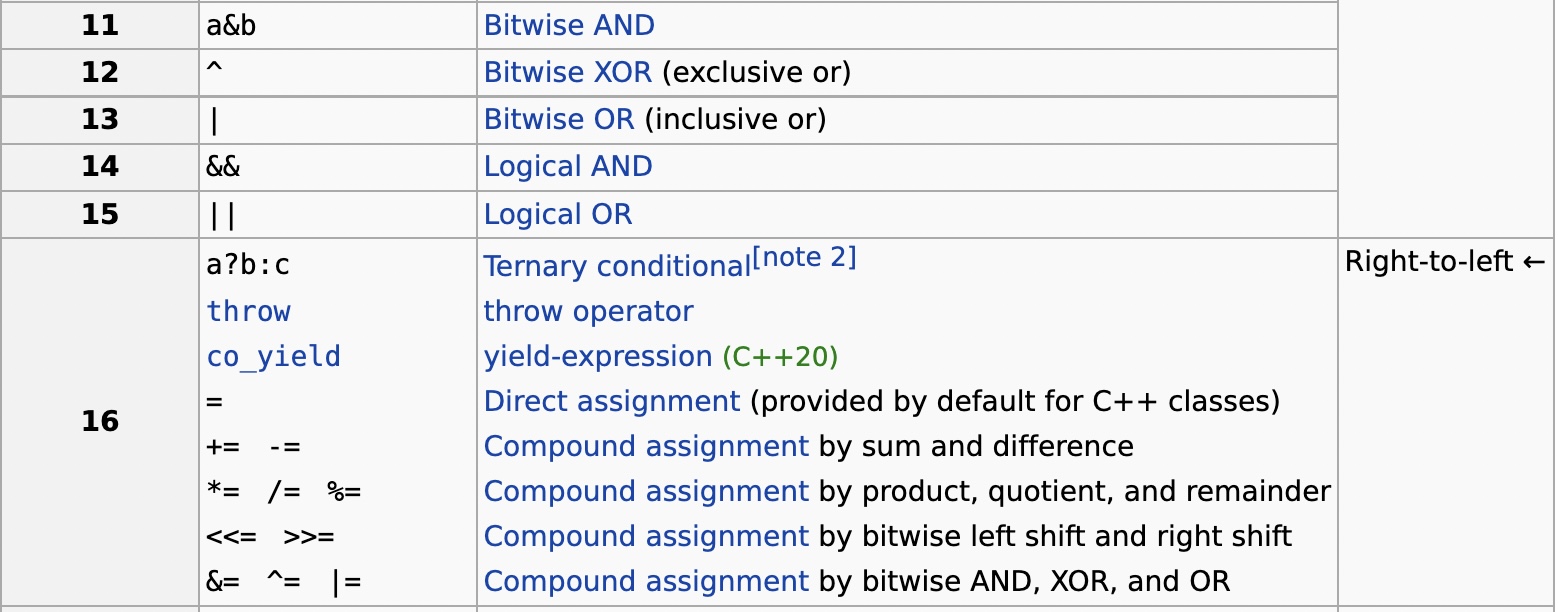
这里要注意一点, 位运算符的优先级要低于比较运算符, 所以位运算最好带上括号, 否则会有意想不到的问题. 下面的运算符优先级表是cppreference1中的.
一个很坑的点就是C语言用与运算判断数字的奇偶性, 奇数的话当然没问题:
#include <stdio.h>
int main(int argc, char const *argv[]) {
int n = 11;
if (n & 1) printf("n is odd\n");
return 0;
}
但是当你加上了一个==0, 情况就发生了变化:
#include <stdio.h>
int main(int argc, char const *argv[]) {
int n = 10;
if (n & 1 == 0) printf("n is even\n");
return 0;
}
10难道不是偶数了? 问题就出在了==和&的优先级上面, ==优先级高, 所以会先计算1==0, 得到了false之后隐式类型转换为0, 这时候10&0肯定就是0了, 才会出现10不是偶数这种错误.
写位运算一定要注意判断语句, 总之就是, 有位运算最好还是都带上括号, 保险.
异或
因为很多题目都主要用到了异或运算, 这里就先谈谈异或.
基本性质
a^b=(a&~b)|(b&~a);a^a=0;a^0=0^a=a;t=x^y$\iff$x^t=x^x^y=y$\iff$y^t=y^x^y=y^y^x=x;
判断两数相乘/除的符号
这里分别针对每一个数进行符号判断当然可以, 但是这里用异或的话一行就可以解决:
int a = 10, b = -12;
int sign1 = (a > 0) ^ (b > 0);
int sign2 = a ^ b < 0; // 这个不太直观
int ans = abs(a) * abs(b) * sign1 ? -1 : 1;
奇偶数的性质
- 加一减一:
x为奇数时:x-1=x^1;x为偶数时:x+1=x^1;
交换两个数
交换两个数应该是最经典也是最基础的一种算法了, 下面是异或实现, 不使用临时变量:
void swap(int a, int b){
a ^= b; // 此时a=a^b,b=b
b ^= a; // 此时a=a^b,b=b^a^b=a
a ^= b; // 此时a=a^b^a=b,b=a
}
或者利用C/C++的连等写法:
void swap(int &a, int &b) { a ^= b ^= a ^= b; }
比较骚的方法.
找不同(数或字符串)
利用异或运算的性质, 遍历一次数组就可以找到结果了(如果是有序数组还可以通过二分来做降低时间复杂度)
例如对于力扣的面试题 17.04. 消失的数字 - 力扣(LeetCode);
用位运算来做简直完美:(求和也可以)
class Solution {
public:
int missingNumber(vector<int>& nums) {
int ans{};
for (int num : nums) ans ^= num;
for (int i = 0; i <= nums.size(); ++i) ans ^= i;
return ans;
}
};
类似还有136. 只出现一次的数字 - 力扣(LeetCode);
class Solution {
public:
int singleNumber(vector<int>& nums) {
int ans{};
for(int num : nums) ans ^= num;
return ans;
}
};
与
判断奇偶
bool isOdd(int n) { return (n & 1) == 1; }
位1的个数(消除最末位)
对于一个二进制串1011001(89), 其中含有的1的个数有多少呢? 一个直观的思路当然是遍历取出, 直接模拟, 例如像下面这样:
class Solution {
public:
int hammingWeight(uint32_t n) {
int ans{};
while (n) ans += (n & 1), n >>= 1;
return ans;
}
};
一些常用的技巧
x & (x - 1) //清除最右边的1
x & -x //得到最右边的1(lsb, 最低有效位)
判断2的幂(数的二进制表示是否仅有一位)
方法1
bool isPow2(int n) { return (n & (n - 1)) == 0; }
对于一个二进制数, 例如10, 其二进制表示为1010, 10-1=9的二进制表示为1001, 两者做与运算得到1000即=8!=0, 但是对于0100(4), 其与3(0011)做与运算就是0, 这是因为对任意一个数x, 其减去1之后得到的二进制数需要从二进制表示的从低位到高位中最近的一个1借位, 使该借位的1后面的所有0都变成1, 那么如果这个数x仅有一个位1的话, 就可得出x&x-1=0了, 反之, 如果数x的二进制表示中不只有一个1, 那么减一操作只会借走最低位的1, 而其他剩下的1就不会变成0, 导致与运算之后结果不为0了.
而一个数字是不是2的幂, 只需要看其二进制表示中是不是只有一个位为1, 于是就可以通过x&x-1==0来判断了.
方法2
bool isPow2(int n) { return (n & (-n)) == n; }
同样地, 我们来分析上面这个式子
找出某数的某一个二进制位
// 获取 a 的第 b 位,最低位编号为 0
int getBit(int a, int b) { return (a >> b) & 1; }
这个和下面的一个技巧都是数位DP中比较常用的设置mask掩码的技巧, 希望大家熟练掌握.
或
某一位设置为1
在数位DP, 状态压缩中常用
// 将 a 的第 b 位设置为 1 ,最低位编号为 0
void setBit(int& a, int b) { a | (1 << b); }
1832. 判断句子是否为全字母句 - 力扣(LeetCode);
这个题当然可以直接哈希完事, 但是需要消耗空间, 这里就通过一个26位的带符号整数(称为mask, 掩码)来完成.
综合运用
大小写转换
比较经典的一类用法, 原理是:
C/C++中, 字符和整数的一一对应关系, 例如:
- 65<=>’A’
- 97<=>’a’
并且 26 个大小写字母 ASCII 码的二进制表示之间存在一个关系: 仅第六位不同.
这个大家可以验证一下:
for i in range(65, 91):
print(bin(i))
for i in range(97, 123):
print(bin(i))
换句话说, 因为同一个字母的大小写之间差了 32 (97-65=32), 这个 32 就代表第六位为 1, 即1<<5=32, 并且仅有 26 个字母, 所以大小写转换其实可以这样写:
auto tolower = [](char c) {
return islower(c) ? c : static_cast<char>(c | 0x20);
};
auto toupper = [](char c) {
return isupper(c) ? c : static_cast<char>(c & ~0x20);
};
当然, 其实不用这么麻烦, C 库函数(ctype.h)里面已经有了 tolower 和 toupper 的实现了, 这里就是玩个花.
用位运算模拟两数相加(异或)
剑指 Offer 65. 不用加减乘除做加法 - 力扣(LeetCode);
这里要用到异或运算的知识, 以及整数补码和溢出情况的分析.
class Solution {
public:
int add(int a, int b) {
if (b == 0) return a;
if (a == 0) return b;
int carry{}, ans{};
while (b) {
carry = (unsigned)(a & b) << 1;
a ^= b; // a加到不进位位置
b = carry;
}
return a;
}
};