题目
给定一个整数 n,计算所有小于等于 n 的非负整数中数字 1 出现的个数。
示例 1:
输入:n = 13 输出:6 示例 2:
输入:n = 0 输出:0
提示:
0 <= n <= 1e9
来源:力扣(LeetCode) 链接:https://leetcode.cn/problems/number-of-digit-one 著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
解题思路
这里面的例子有问题, 说是 0~10^9, 结果早就超出 1e9 了…
首先来看这样一个例子:13, 怎样来计算数字 1 的个数呢?
一个比较直观的思路就是先计算1~10中数字 1 的个数, 然后计算11~13中数字 1 的个数.
显然: 1~10中含有的 1 的个数为 2, 但是在11~13中, 应该怎么计算呢? 这里可以进一步分解计算, 先计算个位中含有 1 的数量, 这里的话就是先计算1~3的 1 的个数, 即为 1, 然后对上一位(即十位1)分类讨论, 如果是 1, 那么 1 的个数就要加上13-10=3, 这样才能计算出总的 1 的个数,即最终的答案为2+1+3=6.
有了这个分析, 我们下面只需要找出计算1~10这样类型的数字 1 个数公式即可, 进一步可以推广为计算:
怎么找出这个公式呢, 先以 100 为例进行分析, 对于 100, $A=1,B=2$, 那么由组合数学的基本计数原理, 对十位和个位中能取到的数进行分类讨论, 对于仅含有 1 个1的数, 1 可以固定在个位或者十位或者百位, 这样的情况有$9\times2+1$个, 这里包含了十位为 0 的情况, 这样就不用额外讨论 10 以内的数了, 最后的1是针对百位而言的, 然后是含有两个1的数, 显然这样的数只有一个, 即11, 那么就可以得到:
这里偷个懒, 我找到了一个计算1~1eN中1的数目的公式, 调用了一下 LeetCode 的提交 API, 即:
证明过程也比较 Trival, 就是幂级数的求导整理运算, 首先通过逐位计算1的数量得到下面的式子,
写成求和的形式, 可得到:
\[f(10^B)=\sum_{k=1}^nk\binom nk9^{n-k}=\sum_{k=0}^n(n-k)\binom nk9^k,\]记
\[g(x)=\sum_{k=0}^n(n-k)\binom nkx^k=(n+1)\sum_{k=0}^n\binom nkx^k-\sum_{k=0}^n\binom nk(k+1)x^k,\]两边对$x$积分得到:
\[\int g(x)\text dx=(1+x)^{n+1}-x(1+x)^n=(1+x)^n\]于是得到:
\[g(x)=n(1+x)^{n-1}\iff f(10^B)=n\cdot10^{n-1}+1.\]但是, 只有这一个例子是不行的, 还不能得到$f(x)$的表达式.(因为 A 需要大等 1)
下面再来看7000这个数, 同100的讨论, 要计算$f(7000)$,需要分别计算仅含有 1 个1的数, 含有两个1的数, 含有三个1的数以及含有 4 个1的数, 可以得到:
这里要注意对首位(本例中为千位)的讨论, 这里的乘以 6 指的是只能选0,2,3,4,5,6这 6 个数, 才能保证 1 的个数确定, 整理一下, 就可以得到最后的结果:
这里在写代码的时候为方便, 直接用 Python 的组合数 API 了, 就是from math import comb, 比较方便, 要是自己写的话也不难, 尾递归实现阶乘然后套公式即可.
代码
from math import comb
class Solution:
def countDigitOne(self, n: int) -> int:
if n == 0:
return 0
def count1(A, B):
if A == 0:
return 0
elif B == 0:
return 1
elif A == 1:
return B * 10**(B - 1) + 1
else:
A -= 1
tmp = 9**B + A * 9**(B - 1) * B + B + 1
for i in range(2, B + 1):
tmp += i * (9**(B - i + 1) * comb(B, i - 1)) + \
i * (A * 9**(B - i) * comb(B, i))
return tmp
def digit(n):
# 计算位数
arr = []
while n:
arr.append(n % 10)
n //= 10
return arr
arr = digit(n)
dgt = len(arr)
ans = 0
flag1 = 0
for i in range(dgt - 1, -1, -1):
ans += count1(arr[i], i)
flag1 += 1 if arr[i] == 1 else 0
if i > 0 and flag1:
ans += arr[i - 1] * flag1 * 10**(i - 1)
return ans
代码部分主要是将数字$n$每一位的位数存成数组, 然后遍历(注意, 这里是逆序), 通过前面的讨论, 判断1所在的位置, 如果有, flag1++, 然后后面的数字都要乘上flag1, 即arr[i - 1] * flag1 * 10**(i - 1).
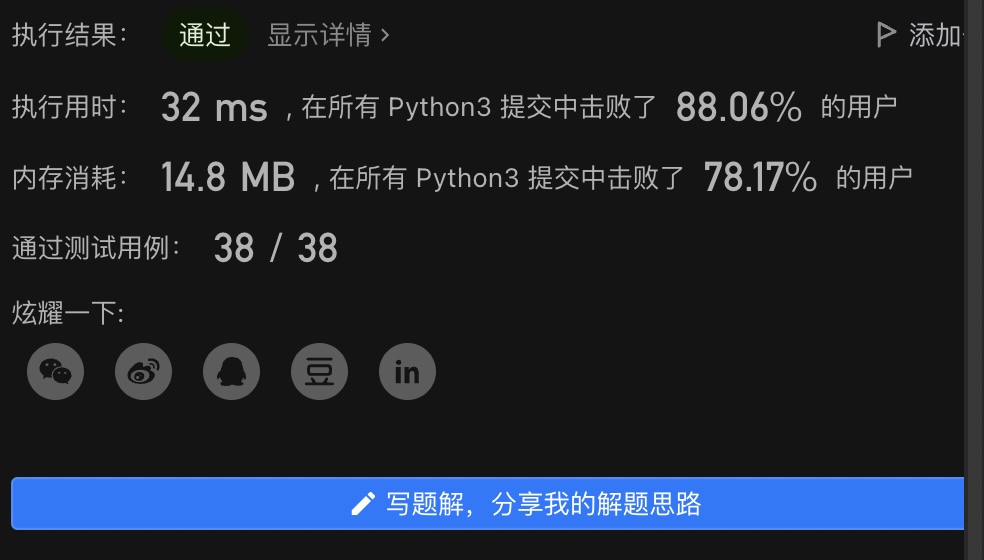
执行结果还是不错的, 算是线性时间了:
小结
因为是我自己通过特例一步一步推的, 就感觉还是比较好理解, 但是这样还是比较费时间, 仅供一乐了, 真正的好方法还得看官解.