写在前面
最近学习偏序集相关理论, 一个主要的内容就是Hasse图, 下面分享一些绘制Hasse图的$\LaTeX$方法1, 主要采用了TikZ和用$\LaTeX$中的$\rm X_{!\Large Y}!!-!!pic$宏包绘制Hasse图, 具体的文档请看
texdoc xy
texdoc xydoc
texdoc xyrefer
texdoc xysource
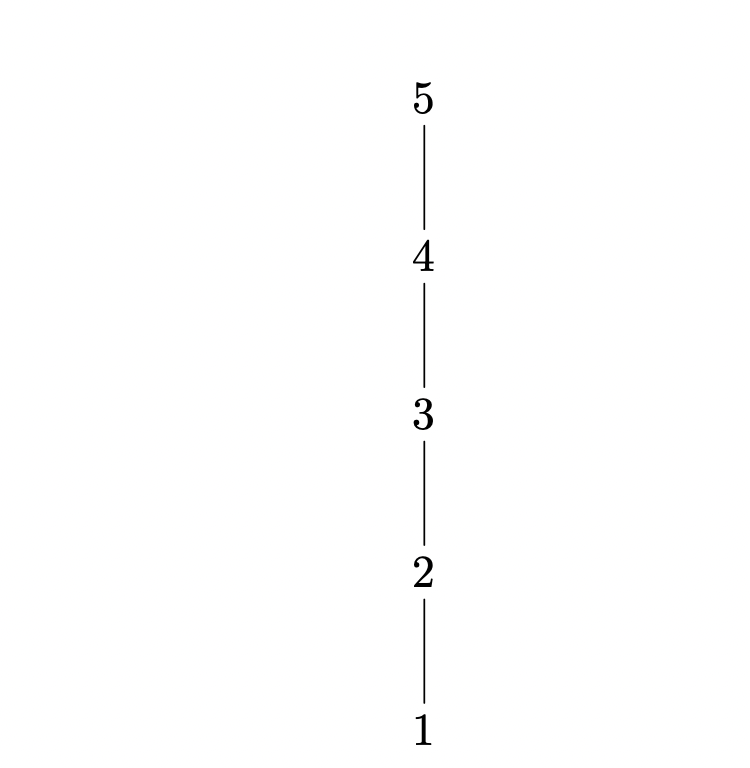
链
这个绘制起来比较简单:
$$
\def\arld{\ar@{-}[d]}
\xymatrix{
5\arld\\
4\arld\\
3\arld\\
2\arld\\
1\\
}
$$
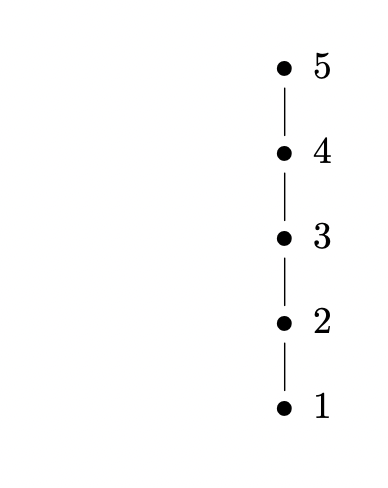
还有一种比较丑的写法:
$$
\newcommand{\B}{\bullet}
\def\arld{\ar@{-}[d]}
\xymatrix@!0{
\B\arld&\hspace{-2.5em}5\\
\B\arld&\hspace{-2.5em}4\\
\B\arld&\hspace{-2.5em}3\\
\B\arld&\hspace{-2.5em}2\\
\B&\hspace{-2.5em}1\\
}
$$
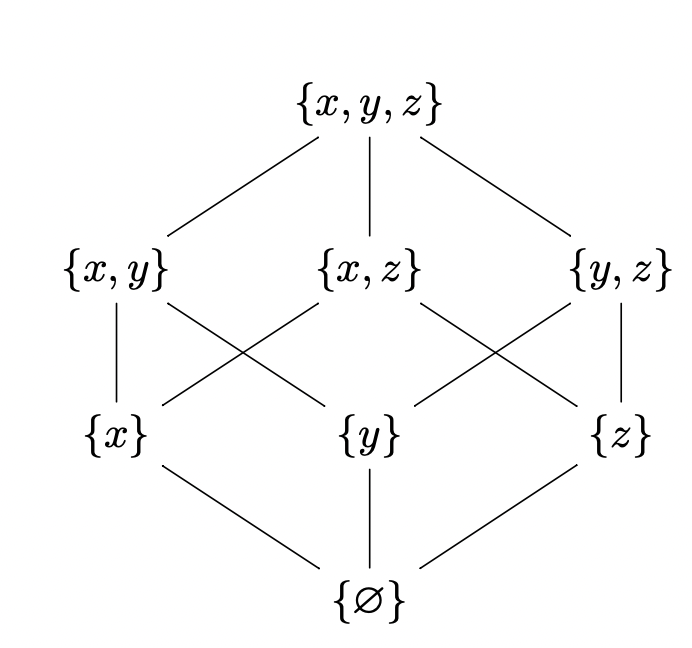
子集格
直接用xy-pic的基本语法就可以:
\documentclass[border=5pt]{standalone}
\usepackage[all,pdf]{xy}
\usepackage{lmodern,amssymb}
$$
\def\arl{\ar@{-}}
\xymatrix{
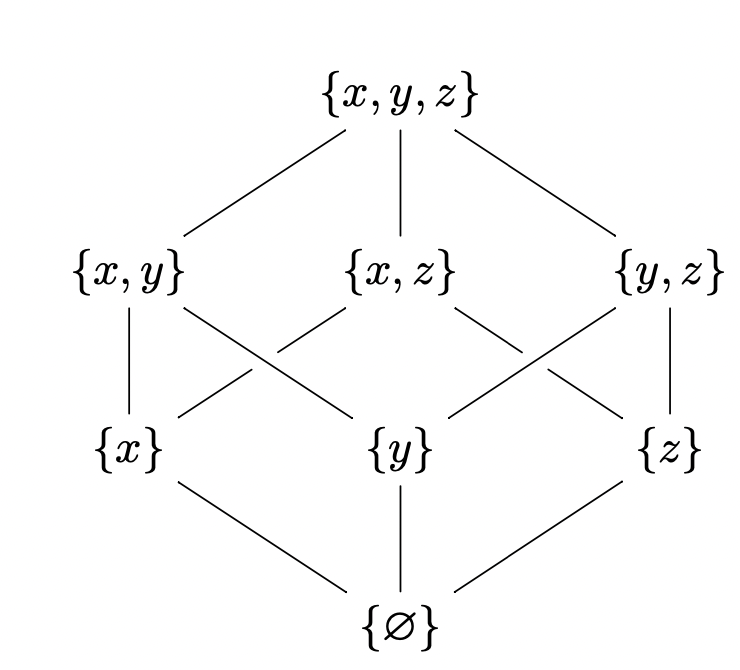
& \{x,y,z\}\arl[dl]\arl[d]\arl[dr] & \\
\{x,y\}\arl[d]\arl[dr] & \{x,z\}\arl[dl]\arl[dr] & \{y,z\}\arl[dl]\arl[d] \\
\{x\}\arl[dr] & \{y\}\arl[d] & \{z\}\arl[dl] \\
& \{\varnothing\} \\
}
$$
加上一点细节(不交叉的线):
$$
\def\arl{\ar@{-}}
\xymatrix{
& \{x,y,z\}\arl[dl]\arl[d]\arl[dr] & \\
\{x,y\}\arl[d]\arl[dr] & \{x,z\}\arl[dl]|\hole\arl[dr]|\hole & \{y,z\}\arl[dl]\arl[d] \\
\{x\}\arl[dr] & \{y\}\arl[d] & \{z\}\arl[dl] \\
& \{\varnothing\} \\
}
$$
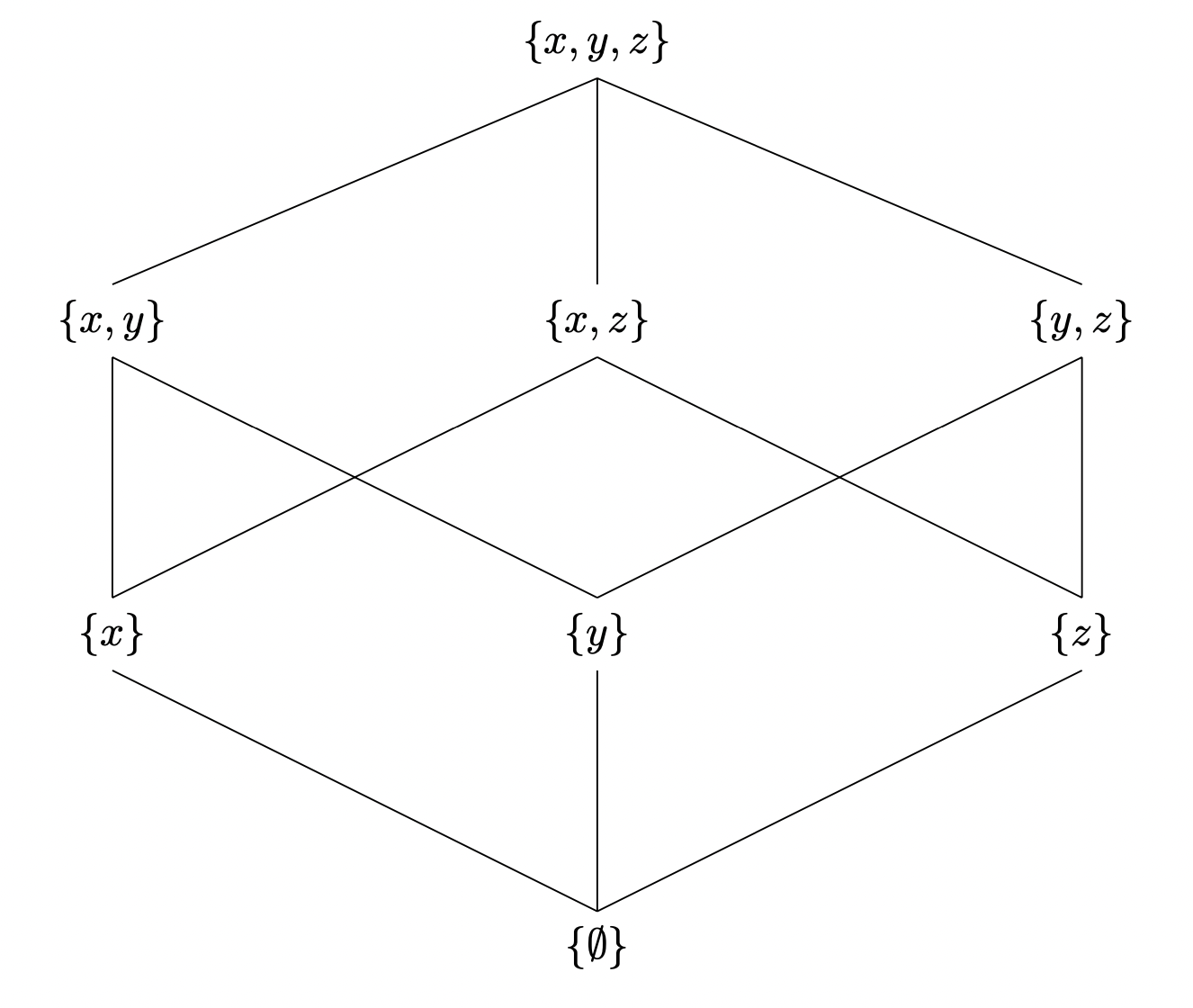
这里提供另一种思路, 参考了Stack Overflow1, 代码显得比较复杂了:
\documentclass[border=5pt,tikz]{standalone}
\usetikzlibrary{matrix}
\begin{document}
\begin{tikzpicture}
\matrix (A) [matrix of nodes, row sep=2cm, nodes={minimum width=4cm}]
{
$\{x,y\}$ & $\{x,z\}$ & $\{y,z\}$ \\
$\{x\}$ & $\{y\}$ & $\{z\}$ \\
& $\{\emptyset\}$ \\
};
\path (A-1-1)--(A-1-2) node[above=2cm] (link) {$\{x,y,z\}$};
\foreach \i in {1,...,3}
\draw (link.south) -- (A-1-\i.north);
\foreach \i/\j in {1/2, 3/2, 2/1, 1/1, 3/3, 2/3}
\draw (A-1-\i.south)--(A-2-\j.north);
\foreach \i/\j in {1/2, 2/2, 3/2}
\draw (A-2-\i.south)--(A-3-\j.north);
\end{tikzpicture}
\end{document}
因子格
旧版本的命令:
\documentclass[border=5pt]{standalone}
\input xypic
\begin{document}
% 这个只能用于旧版本的xy-pic命令
$$
\diagram
12 & 20 \\
4\uline \urline & 10 \uline & 25 \\
2 \uline \urline & 5 \uline \urline
\enddiagram
$$
\end{document}
这个是新版本的导入与绘制命令:
\documentclass[border=5pt]{standalone}
\usepackage[all]{xy}
\begin{document}
$$
\xymatrix{
12 & 20 \\
4 \ar@{-}[u] \ar@{-}[ur] & 10 \ar@{-}[u] & 25 \\
2 \ar@{-}[u] \ar@{-}[ur] & 5 \ar@{-}[u] \ar@{-}[ur]
}
$$
% 也可简写为:
$$
\def\arl{\ar@{-}}
\xymatrix{
12 & 20 \\
4 \arl[u] \arl[ur] & 10 \arl[u] & 25 \\
2 \arl[u] \arl[ur] & 5 \arl[u] \arl[ur]
}
$$
\end{document}
生成的结果如图:
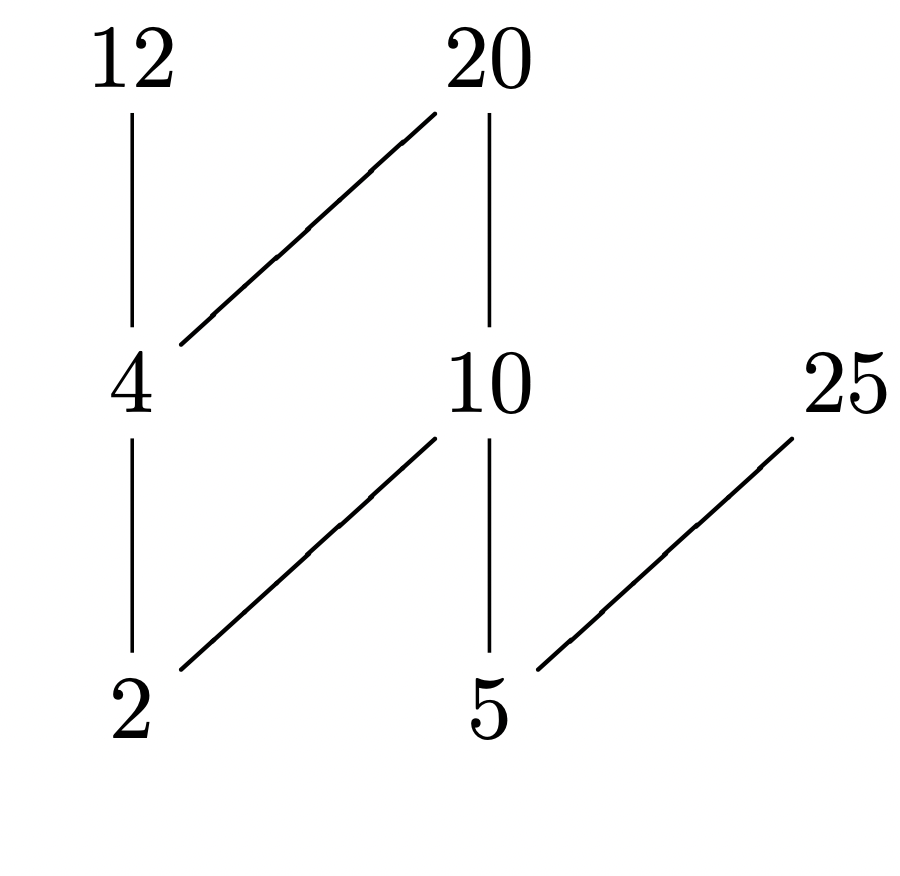
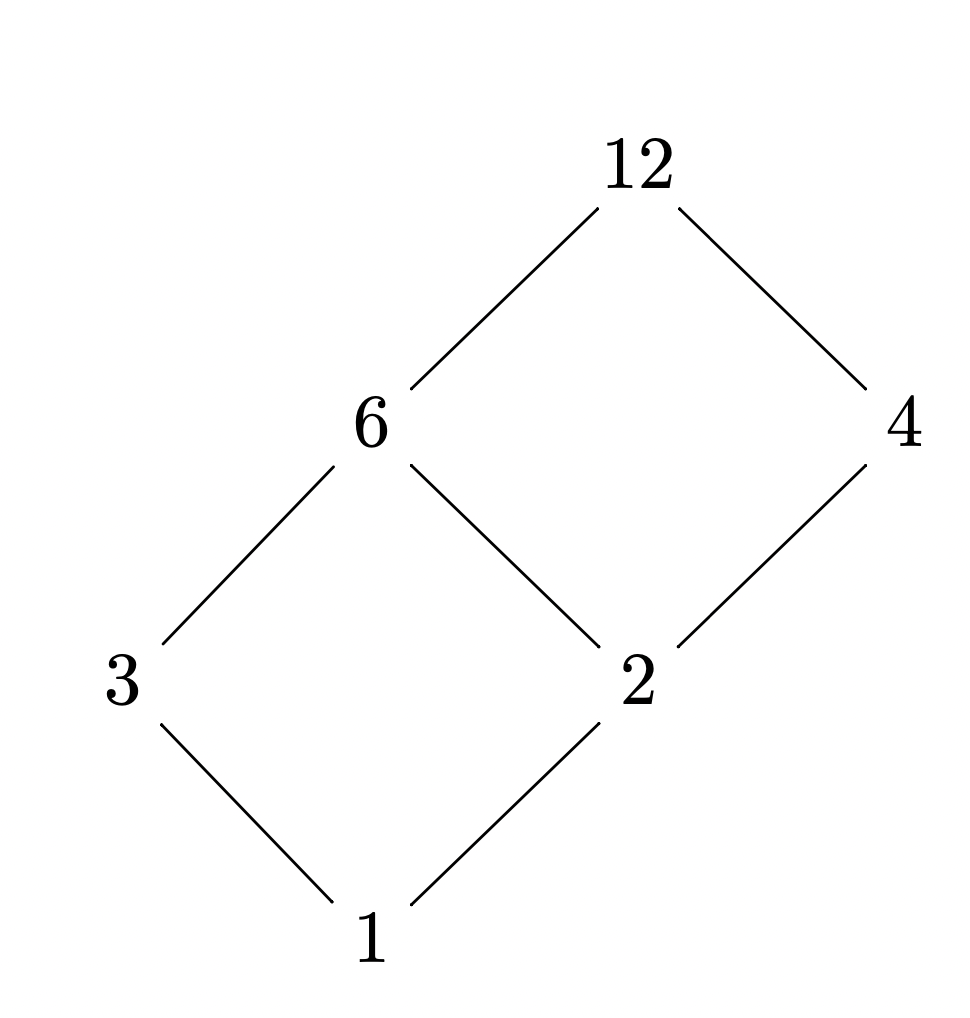
对$12$来说的因子格:
$$
\def\arl{\ar@{-}}
\xymatrix{
& & 12\arl[dl]\arl[dr] & \\
& 6\arl[dl]\arl[dr] & &4\arl[dl]\\
3\arl[dr] & &2\arl[dl] & \\
&1&&\\
}
$$