现代图论笔记(二)树与二分图

Category： Maths

写在前面

这次介绍一些树和二分图的定义和主要性质, 以及这两种结构中常用的算法, 包括二分图的判定, 最小生成树的寻找等.

好久才更新, 只能说自己的代码能力还有欠缺, 一些算法知道思路但就是写不出来.

基本概念

无圈图(acyclic graph): 任何子图都不是圈的图.
树(tree): 连通的无圈图.
森林(forest): 指所有连通分量都是树的图.
二叉树(): 一棵有根树, 其每个结点至多有两个孩子.
完全二叉树: 除叶子结点外的其他所有节点都有两个孩子的有根二叉树.
叶结点: 度为1的结点(一称端节点, 移除端节点之后原图仍是树).
桥(bridge): 一个连通图若删除某条贬值后变为非连通的, 被删除的边称为桥.

生成树: 对于一个给定的连通图$G$, 其某个生成子图为一棵树.
生成树的权重: 即图对应的权重(边).
生成树的$k-$差($k-$deficient)结点: 设$v$是图$G$的生成树中的结点, 若其度数满足 $\deg_G(v)-\deg_T(v)=k,$
结点$v$的差额(deficiency: $k$.
- $k=0$: 度保持结点, 即$\deg_G(v)=\deg_T(v)$.

二部图: 图$G$的结点集$V(G)$可以分为两个非空子集$V_1$和$V_2$, 且满足$G$的边$xy$关联的两个结点$x,\,y$分别属于这两个子集. (所有的树都是二分图)
二分图的分类:
\[\begin{cases} |V_1|=|V_2|&:\ \text{平衡二部图}\\ |V_1|-|V_2|=1&:\text{准平衡二部图}\\ |V_1|-|V_2|\geq2&:\text{偏斜二分图} \end{cases}\]

图的匹配$M$: 由一些边组成的集合, 其中的任何两个边不关联.
从$X$到$Y$的完全匹配: 若$X$中的每个结点都关联于匹配$M$中的一条边.
完美匹配: 匹配$M$是从$X$到$Y$的一个完全匹配, 同时也是$Y$到$X$的一个完全匹配.
最大匹配: 匹配$M$在图$G$的所有匹配中基数最大.
极大匹配: 不存在更大的匹配$M’$包含匹配$M$.
$M-$交错路: 由在$M$中的边和不在$M$中的边交替出现构成.
$M-$增广路: 连接两个$M-$不匹配结点的交错路. 其开始并终止于不在$M$中的边.

树的重要性质

每个非平凡树(平凡图$K_1$也是树)至少有两个端节点(叶子结点).
删除树的任意一条边(即: 桥)都会使树变为非连通图. (对于费连通图来说, 删除某边如果增加连通分量数量, 这条边也称为图的桥)
对树的任意给定的两个节点$x, \,y$, 树中存在唯一一条路$x-y$, 因此, 此路为测地线.
有$n$个结点的树, 其必有$n-1$条边, 因此, 树是最小连通的.

度序列

设$S$为$n$个正整数组整的序列$d_1,d_2,…,d_n$, 其中, $d_1\geq d_2\geq…\geq d_n$, 且$d_1+d_2+\cdots+d_n=2(n-1)$, 则存在一个树, 其度序列为$S$.

证明思路: 数学归纳法, 主要采用删边加边的方式进行, 需要注意的是这里要删去的边以及结点要满足是叶子结点.

树的叶子数

对非平凡树$T$, 度为$i$的结点数记为$n_i$, 其叶子数满足

\[n_1=2+n_3+2n_4+3n_5+\cdots=2+\sum_{i=3}^\infty(i-2)n_i.\]

证明思路: 将树绘制成一棵有根树, 根节点为叶子结点(端节点), 先考虑任何一条从根节点到任一叶结点的一条路, 于是度为1的结点数目加上2. 对任何度大于2的结点, 其度减去2正好是该结点中多出来的边, 这样的边一定可以找到叶子结点, 所以只需考虑这样的结点对叶结点的贡献即可.

最小生成树

对含有$n$个结点, $q$条边的连通图$G$构造生成树, 必须删除$q-(n-1)=q-n+1$条边, 其中删除的任何一条边都不能是桥.
含$n$个结点, $q$条边的连通图$G$, 其生成树的所有结点的差额和为$2(q-n+1)$.

证明思路:

直接从图中所有结点的度之和$2q$减去生成树的结点的度之和$2(n-1)$即得到: $\text{差额和}=2q-2(n-1)=2(q-n+1).$
最小(代价)生成树: 图$G$的所有边上的权重(代价)之和最小的生成树.

二分图与最大匹配问题

不含奇圈$\iff$二分图.
树: 二分图.
图$G$的匹配$M$是最大匹配当且仅当$G$中没有$M-$增广路

Hall匹配定理

该定理在组合方面有重要的应用, 但是这里主要采用图论的语言来叙述并证明.

对于结点$v$, 用$n(v)$表示所有与$v$邻接的结点集, 对于图$G$结点集任意子集$S$, $N(S)$表示所有与$S$中结点相邻接的结点集的并集, 即有

\[N(S)=\bigcup_{v\in S}n(v).\]

定理: 二分图$G$的两个部分为$X, Y$, 若存在从$X$到$Y$的完全匹配当且仅当对$\forall S\subseteq X$, 有$

N(S)

\geqslant

(相异性条件)$.

二分图$G$的两个部分为$X, Y$, 满足$

$时, 图$G$存在完美匹配$\iff$对任意子集$S\subseteq X$有$

N(S)

\geq

正则二分图一定平衡. ($ X = Y $).
正则二分图一定存在完美匹配.

算法与实现

二分图的判定

在此过程中, 用$a$和$b$表示相反的标号

任取一结点, 标记为$a$
所有与$a$邻接的结点标记为$b$
对任意已标记的结点$v$, 将所有与$v$邻接且未标记的结点标记为与$v$相反的标号.
重复步骤3, 直到不存在与已标记结点邻接且还未标记的结点.
如果图中还有未标记结点, 那么, 这些结点一定在一个新的连通分量中, 再选择其中一个结点标记为$a$, 转到步骤3.
如果得到的图中, 所有邻接的结点都标记为不同的标号, 那么图$G$就是二分图. 设集合$V_1$为二分图中所有标记为$a$的结点集;集合$V_2$为二分图中所有标记为$b$的结点集. 如果存在一对邻接点标记为同样的标号, 那么图$G$就不是二分图.

采用Python实现, 图的存储使用邻接表实现.

def isBipartite(graph) -> bool:
    """
    未染色: 0
    染红色: 1
    染绿色: -1
    """
    n = len(graph)
    color_vec = [0] * n

    def dfs(i, color):
        for it in graph[i]:
            if color_vec[it] == 0:
                # 如果未染色, 进行染色
                color_vec[it] = -color
                if not dfs(it, -color):
                    # 染色后dfs判断
                    return False
            elif color_vec[it] == -color:
                # 满足条件进行下一轮遍历
                continue
            else:
                return False
        return True

    for i in range(n):
        if color_vec[i] == 0:
            # 说明存在新的连通分支, 进行dfs
            if not dfs(i, r):
                return False
    return True


if __name__ == '__main__':
    # 采用邻接表的方式存储图
    g1 = [[1, 2], [0, 2, 3], [0, 1, 3], [1, 2]]
    g2 = [[1], [2, 3], [4], [0, 4], [1]]
    g3 = [[1, 3], [0, 2], [1, 3], [0, 2]]
    print(isBipartite(g1))
    print(isBipartite(g2))
    print(isBipartite(g3))
'''输出结果:
False
False
True
'''

寻找最小生成树

Kruskal算法(核心: 贪婪算法)

每一步都选取最小权重的边, 并且保证每一次加入边之后都不会形成圈.

先将边按照权重从小到大的顺序存放在表$L$中(权重相同的边按字母表顺序)

$S=\varnothing$.
在已排好的表$L$中的下一条边$e$，若$R \notin S$且导出子图 $\langle S\cup {e} \rangle$是无圈图，则令$S = S \cup {e}$.
若 $ S =n-1$ , 则算法停止，输出集合$S$，否则转第2步，继续遍历表$L$.

证明算法的合理性主要思路:

步骤2保证得到的图无圈, 步骤3保证得到$n-1$条边时候算法终止.

反证, 假设通过Kruskal算法得到的树不是代价最小的, 则必定存在一个代价更小的生成树, 通过比较权重, 以及加边删边操作得到矛盾.

代码¹:

from math import inf as X
# import numpy as np
from adjacent_matrix_table_with_weights import matrix2list


class edge:
    """边:首结点initial尾结点end权重weight"""

    def __init__(self, initial, end, weight):
        self.initial = initial
        self.end = end
        self.weight = weight


# 克鲁斯卡尔算法寻找最小生成树
def kruskal_MinTree(N, P, edges):
    # 保存最小生成数各个边的信息
    minTree = []
    # 记录选择边的数量
    num = 0
    # 为每个顶点添加标记
    assists = [i for i in range(N)]
    # 对 edges 列表进行排序
    edges.sort(key=lambda x: x.weight)
    # 遍历边, 选择可组成最小生成树的边
    for i in range(P):
        # 找到当前边的两个顶点在 assists 数组中的位置下标
        initial = edges[i].initial
        end = edges[i].end
        # 判断: 不会产生回路
        # 如果顶点的标记不同, 说明不在一个集合中
        if assists[initial] != assists[end]:
            # 记录该边, 作为最小生成树的组成部分
            minTree.append(edges[i])
            # 计数+1
            num += 1
            # 将新加入生成树的顶点标记全部改为一样的
            elem = assists[end]
            for k in range(N):
                if assists[k] == elem:
                    assists[k] = assists[initial]
            # 如果选择的边的数量和顶点数相差1, 证明最小生成树已经形成, 退出循环
            if num == N - 1:
                break
    return minTree


graph1 = [
    [0, 2, X, X, X],
    [2, 0, X, 3, 2],
    [X, X, 0, X, 1],
    [X, 3, X, 0, 4],
    [X, 2, 1, 4, 0]
]
'''
最小生成树为:
2-4  权值: 1
0-1  权值: 2
1-4  权值: 2
1-3  权值: 3
总权值为:8
'''

# arr = np.array(graph)
# N = int(np.max(arr[arr != X])) + 1
# P = np.count_nonzero(arr[arr != X]) // 2


def getNP(graph):
    # 结点数
    N = len(graph)
    # 边数
    P = 0
    for i in range(N):
        for j in range(i):
            P += (graph[i][j] != X)
    return N, P


# adjacent_list = matrix2list(graph1)
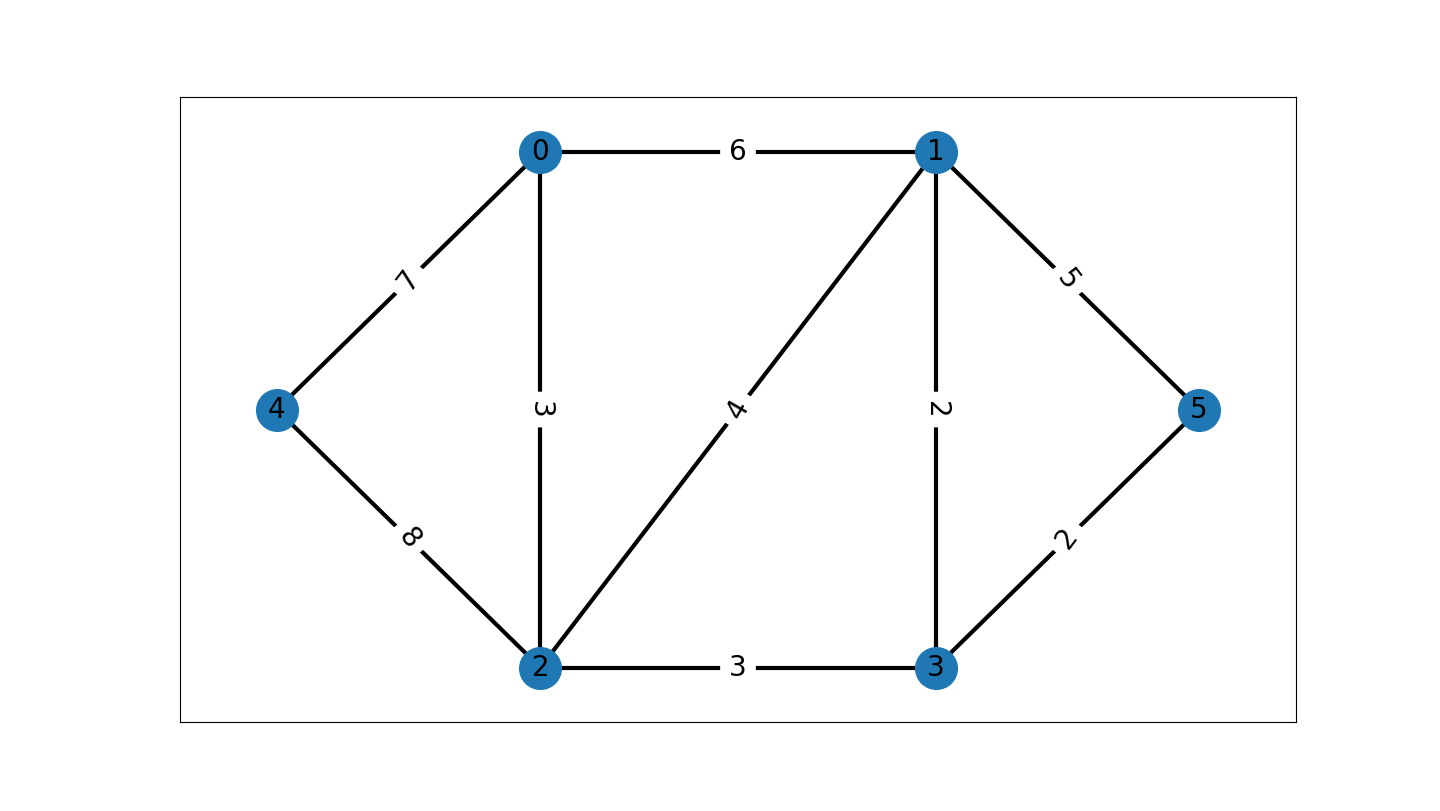
mat1 = [[0, 7, 8, X, X, X],
        [7, 0, 3, 6, X, X],
        [8, 3, 0, 4, 3, X],
        [X, 6, 4, 0, 2, 5],
        [X, X, 3, 2, 0, 2],
        [X, X, X, 5, 2, 0]]
"""
图的结点数为:  6 边数为:  9
最小生成树为:
3-4  权值: 2
4-5  权值: 2
1-2  权值: 3
2-4  权值: 3
0-1  权值: 7
总权值为:17
"""
N, P = getNP(mat1)
print("图的结点数为: ", N, "边数为: ", P)

lst1 = matrix2list(mat1)
edges = []   # 用于保存用户输入的图各条边的信息

# # 输入 N 条边的信息
for (initial, end), weight in lst1:
    edges.append(edge(initial, end, weight))

# 执行算法添加边到结果列表
minTrees = kruskal_MinTree(N, P, edges)

cost = 0
print("最小生成树为:")
for i in range(N - 1):
    print("%d-%d  权值: %d" %
          (minTrees[i].initial, minTrees[i].end, minTrees[i].weight))
    cost = cost + minTrees[i].weight
print("总权值为:%d" % (cost))

Prim算法(核心: 广度优先算法)

选出结点 $v$，令$V(T)={v},\,E(T)=\varnothing$.
在所有 $u \notin V(T),\,w\in V(T)$ 的结点中, 若连接结点 $u$ 和 $w$ 的边 $e=uw$是最小权重边, 则令$V (T) = V(T)\cup{u},\,E(T) =E(T) \cup {uw}$.
若 $ E(T) =n-1$ , 算法停止, 输出 $E(T)$ , 否则, 转向步骤2, 向树中增加新的结点.

代码²:

from math import inf as X


def min_Key(N, key, visited):
    """查找权值最小且尚未被选择的顶点, key 列表记录了各顶点间的权值"""
    # min_weight 记录最小的权值, min_index 记录最小权值关联的顶点
    min_weight = X
    min_index = 0
    # 遍历 key 列表
    for i in range(N):
        # 如果当前顶点未被选择, 且对应的权值小于 min_weight
        if not visited[i] and key[i] < min_weight:
            # 更新 min_weight 的值并记录该顶点的位置
            min_weight = key[i]
            min_index = i
    # 返回最小权值的顶点的位置
    return min_index


def prim_MinTree(N, cost):
    # key 列表用于记录顶点权值
    # parent 列表用于记录最小生成树中各个顶点父节点的位置
    # visited记录各顶点是否已经被选择(属于 A 类还是 B 类)
    # A类代表已经存入生成树的结点, B类表示还未遍历的结点
    parent = [-1] * N
    key = [X] * N
    visited = [False] * N
    # 选择 key 列表中第一个顶点, 开始寻找最小生成树
    key[0] = 0
    # |E(T)| = N - 1
    for _ in range(N - 1):
        # 从 key 列表中找到权值最小的顶点所在的位置
        u = min_Key(N, key, visited)
        visited[u] = True
        # 由于新顶点加入 A 类, 因此需要更新 key 列表中的数据
        for v in range(N):
            # 如果类B(未被遍历)中存在到下标为u的顶点权值(不为0)比 key中记录的权值还小
            # 表明新顶点的加入, 使得类 B 到类 A 顶点的权值有了更好的选择
            if cost[u][v] and not visited[v] and cost[u][v] < key[v]:
                # 更新 parent记录的各个顶点父节点的信息
                parent[v] = u
                # 更新 key 列表
                key[v] = cost[u][v]
    # 根据 parent 记录的各个顶点父节点的信息
    return parent


def getNP(graph):
    # 结点数
    N = len(graph)
    # 边数
    P = 0
    for i in range(N):
        for j in range(i):
            P += (graph[i][j] != X)
    return N, P


cost = [[0, 7, 8, X, X, X],
        [7, 0, 3, 6, X, X],
        [8, 3, 0, 4, 3, X],
        [X, 6, 4, 0, 2, 5],
        [X, X, 3, 2, 0, 2],
        [X, X, X, 5, 2, 0]]
N, P = getNP(cost)
print("结点数为: ", N, "边数为: ", P)

parent = prim_MinTree(N, cost)
# print(parent)
# [-1, 0, 1, 4, 2, 4]

minCost = 0
print("最小生成树为：")
# 遍历 parent 列表
for i in range(1, N):
    # parent 列表下标值表示各个顶点, 各个下标对应的值为该顶点的父节点
    print("%d - %d wight:%d" % (parent[i], i, cost[i][parent[i]]))
    # 统计最小生成树的总权值
    minCost = minCost + cost[i][parent[i]]
print("总权值为：%d" % (minCost))
'''
结点数为:  6 边数为:  9
最小生成树为：
0 - 1 wight:7
1 - 2 wight:3
4 - 3 wight:2
2 - 4 wight:3
4 - 5 wight:2
总权值为：17
'''

代码参考

上篇不改变分辨率转换pdf为png图片方法汇总

下篇英语课小记(一)