组合学笔记(一)偏序集概念与应用

Category： Maths

写在前面

最近看论文需要用到偏序集的有关概念, 在这里先梳理一下, 方便以后的使用. 主要参考的书籍是Stanley的经典名著《计数组合学(第一卷)》.

下面若不特别指明, 均用$P$代表偏序集.

定义

偏序集(partially-ordered set, poset)$P$是一个集合, 连同一个记为$\leq$($\leq_P$)的二元关系, 满足下面的三条公理:

对所有的$x\in P$, $x\leq x$(自反性).
如果$x\leq y$ 且$y\leq x$, 则$x=y$(反对称性).
如果$x\leq y$且$y\leq z$, 则$x\leq z$(传递性).

偏序集$P$中的两个元素$x,y$可比, 如果$x\leq y$或者$y\leq x$, 否则称其为不可比的.
偏序集$P,Q$同构: $P,Q$之间存在一个保持序关系的双射$\phi:\ P\longrightarrow Q$使得他的逆也保持序关系. 即: $在P中x\leq y\iff 在Q中\phi(x)\leq\phi(y).$

弱子偏序集: 偏序集$P$的子集$Q$连同$Q$上满足”如果在$Q$中有$x\leq y$, 则在$P$中$x\leq y$“的偏序关系, 则$Q$为$P$的弱子偏序集.
加细: 若$Q$是$P$的弱子偏序集, 且作为集合有$P=Q$, 则称$P$是$Q$的加细.
诱导子偏序集: $P$的子集连同$Q$上的偏序关系:”$\forall x,y\in Q$, 在$Q$中有$x\leq y\iff$在$P$中有$x\leq y$”.
诱导序: $Q$是$P$的诱导子偏序集, 则$Q$具有诱导序. 有限偏序集$P$恰好有$2^{ P }$个诱导子偏序集.
局部有限偏序集: 偏序集$P$的任一区间都是有限的. (可完全由其覆盖关系所确定)
凸子偏序集: 若在偏序集$P$中有$x<y<z$且$x,z\in Q$, 就有$y\in Q$, 此时区间也是凸的.

$y$覆盖$x$: 设$x,y\in P$, 若$x<y$且不存在$z\in P$使得$x<z<y$. 充要条件:$x<y$且$[x,y]={x,y}$.
(有限偏序集的)Hasse图: 顶点为$P$中元素, 边为覆盖关系, 并且若$x<y$则$y$绘制在$x$”上面”的图形.

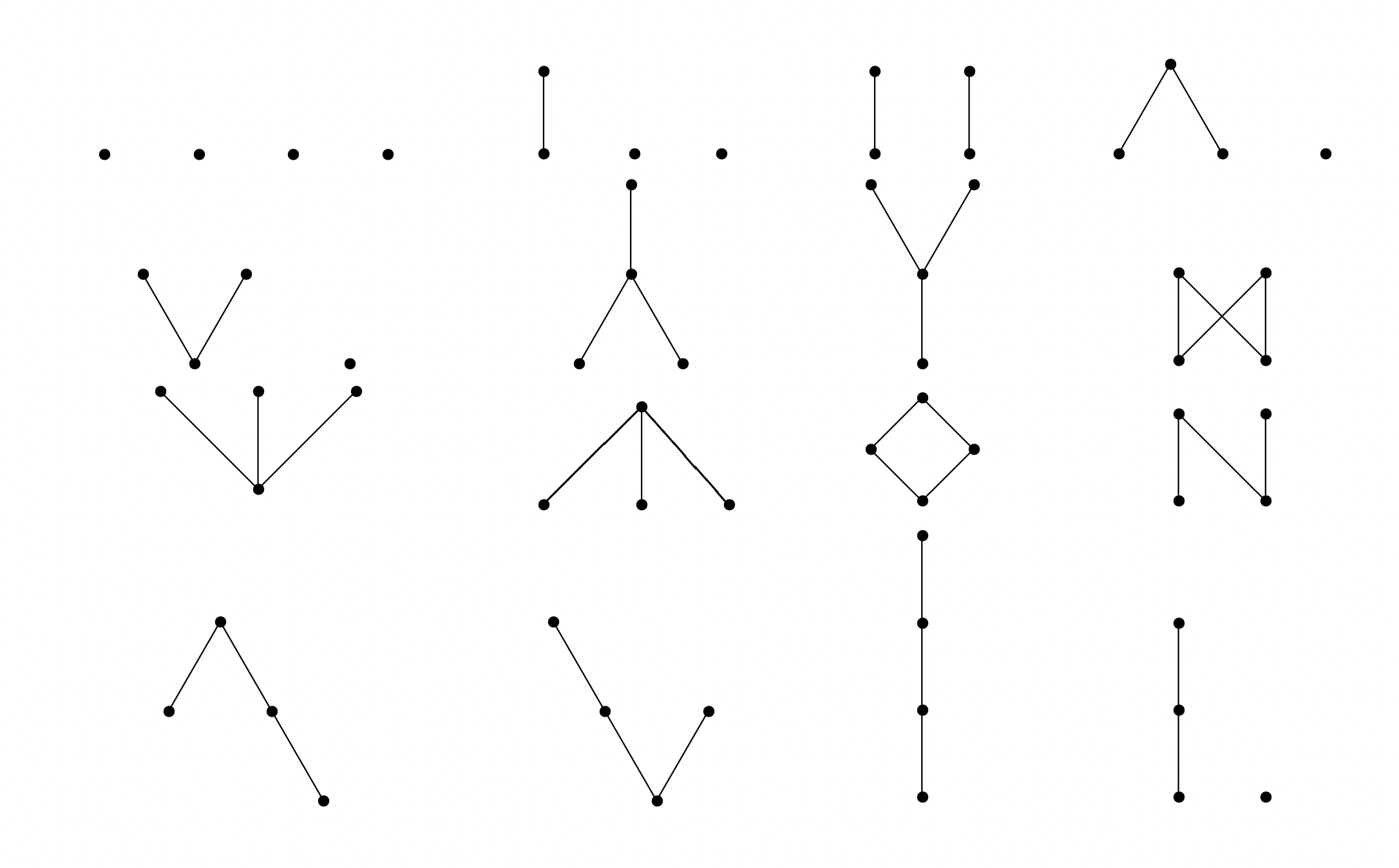
Hasse图的一些例子, 可以参考我的前面的博客. 含有四个元素的偏序集有16个, Hasse图如下图所示

偏序集$P$具有$\hat 0$: 若存在某个元素$\hat0\in P$使得对所有的$x\in P$都有$x\geq \hat0$.
偏序集$P$具有$\hat 1$: 若存在某个元素$\hat1\in P$使得对所有的$x\in P$都有$x\leq \hat1$.
$\hat P$: 表示在$P$中加入$\hat0,\hat1$得到的偏序集(不管$P$本身是否含有$\hat0$和$\hat1$).

若$x,y\in P$, 那么$x,y$的上界为满足$z\geq x,z\geq y$的元素$z\in P$.
$x,y$的最小上界为$x,y$的上界$z$, 使得对$x,y$的每一个上界$w$, 都有$w\geq z$.
若$x,y$最小上界存在, 则唯一, 记为$x\vee y$, 同理, 最大下界记为$x\wedge y$.
格(lattice): 是一个偏序集$L$, 其中每一对元素的最小上界和最大下界都存在.
格满足的一些性质:
\[\begin{cases}a.运算\vee,\wedge是结合,交换,幂等的\\b. x\wedge(x\vee y)=x=x\vee(x\wedge y)\\c. x\wedge y=x\iff x\vee y=y\iff x\leq y\end{cases}\]

链(chain, 全序集,线性序集)

指任意两个元素都可以比较大小的偏序集. 例如$[n]={1,2,…,n}$及其上的普通序关系, 记为$\mathbf {n}$.
偏序集$P$的子集$C$为链, 若$C$ 作为$P$的子偏序集的时候是链.
偏序集$P$中的链$C$为饱和的(不可加细的), 如果不存在$z\in P-C$使得对于$C$中某两个元素$x,y$有$x<z<y$, 并且$C\cup{z}$仍然构成链. (有点像上确界的定义, 没办法再塞进去一个元素)
局部有限偏序集中的链$x_0<x_1<\cdots<x_n$是饱和的, $\iff$对$1\leq i\leq n$有$x_i$覆盖$x_{i-1}$.
有限链的长度$\ell(C):=\ell(C)= C -1$.
$\bigstar$有限偏序集$P$的长度(秩)定义为$\ell(P):=\max{\ell(C):\ C为P的链}$.
偏序集的区间$[x,y]$的长度记为$\ell(x,y)$.
$\bigstar$秩为$n$的分次偏序集: 若偏序集$P$的所有极大链都具有相同长度$n$. 此时存在唯一秩函数$\rho:P\longrightarrow{0,1,…,n}$, 满足:
1. 若$x$是$P$的极小元, 则$\rho(x)=0$;
2. 若在$P$中有$y$覆盖$x$, 则$\rho(y)=\rho(x)+1$.
如果$\rho(x)=i$, 称元素$x$具有秩$i$.
$\bigstar$偏序集的秩生成函数: 对秩为$n$的分次偏序集$P$, 其中有$p_i$个元素的秩为$i$, 则$P$的秩生成函数为: $F(P,q)=\sum_{i=0}^np_iq^i.$
偏序集的可重链: 具有重复元素的链, 即基集为$P$的某个链的可重集合.
反链(Sperner族, 集群): 偏序集$P$的子集$A$, 其中任意两个不同元素不可比较.

序理想

$P$的序理想(半理想, 下集, 下降子集): 满足下列条件的$P$的子集. (有点像左开右闭区间)
\[若x\in I 且 y\leq x, 则y\in I.\]
对偶序理想(滤子): 满足下列条件的$P$的子集. (有点像左闭右开区间) $若x\in I 且 y\geq x, 则y\in I.$
偏序集$P$有限时, $P$的反链$A$和序理想$I$之间存在一一对应. 也就是说, $A$为$I$的极大元构成的集合, 而 $I=\{x\in P:\ 对某个y\in A有x\leq y\}.\tag{*}$
偏序集$P$的所有序理想按照包含关系排序, 构成一个偏序集, 记为$J(P)$.
$A$生成$I$: 若序理想$I$和极大元所成集合$A$之间满足$(*)$式. 若$A={x_1,…,x_k}$, 记$I=\langle x_1,…,x_k\rangle$为由$A$生成的序理想.
主序理想: 序理想$\langle x\rangle$为由$x$生成的主序理想, 记为$A_x$.
主对偶序理想: $V_x={y\in P:\ y\geq x}$表示由$x$生成的主对偶序理想.

偏序集上的运算

直和(不交并): 即定义在$P\cup Q$上的偏序集, 记为$P+Q$, 指两不相交集合$P,Q$上定义的偏序集, 使得在$P+Q$中有$x\leq y$.
- 即在$P+Q$中, 或者有$\forall x,y\in P,x\leq_P y$, 或者有$\forall x,y\in Q,x\leq_Q y$.
- 若一个偏序集不是两个非空偏序集的不交并, 这称之为连通的.
- $P$ 和自身的$n$次不交并记为$nP$.
- 一个$n$元反链同构于$n\mathbf{1}$.
有序和: 即定义在$P\cup Q$上的偏序集记为$P\oplus Q$, 使得在$P\oplus Q$中$x\leq y$.
- 即在$P\oplus Q$中, 或者有$\forall x,y\in P,x\leq_P y$, 或者有$\forall x,y\in Q,x\leq_Q y$, 或者有$x\in P,y\in Q$.
- 一条$n$元链由$\bf n=\underbrace{1\oplus1\oplus\cdots\oplus1}_{\mathrm n\text{个}}$给出.
- 串并联偏序集: 在$16$个四元偏序集中, 恰有一个是不能由偏序集$\bf1$通过直和运算与有序和运算构造出来.
  
  这个偏序集为上图中的第二行的最后一个, 显然他不能够通过直和以及有序和运算生成.
直积(笛卡尔积): 定义在集合${(x,y):\ x\in P,y\in Q}$上的偏序集$P\times Q$, 满足在$P\times Q$中有$(x,y)\leq (x’,y’)$.
- 即$\forall x,x’\in P,x\leq_P x’$, $\forall y,y’\in Q,y\leq_Q y’$.
- $P$和它自身的$n$次直积记为$P^n$.
- $P\times Q\cong Q\times P$.
- 如果$P,Q$是分次的且秩生成函数为$F(P,q)$和$F(Q,q)$, 则$P\times Q$也是分次的且:
  \[F(P\times Q,q)=F(P,q)F(Q,q).\]
有序积: $P\otimes Q$, 定义在${(x,y):\ x\in P,y\in Q}$上, 满足$(x,y)\leq (x’,y’)$, 若$x=x’$且$y\leq y’$, 或$x<x’$.
- 如果$P,Q$是分次的并且$Q$的秩为$r$, 则对于有序积, 有
  \[F(P\otimes Q,q)=F(P,q^{r+1})F(Q,q).\]
对偶(dual): 记为${P^}$, 是与$P$定义在同一集合上的偏序集$P^$, 但在$P^$中$x\leq_{P^} y\iff y\leq_P x$.
- 自对偶: $P\cong P^*$.
  - 下面是所有含四个元素的偏序集中的自对偶图
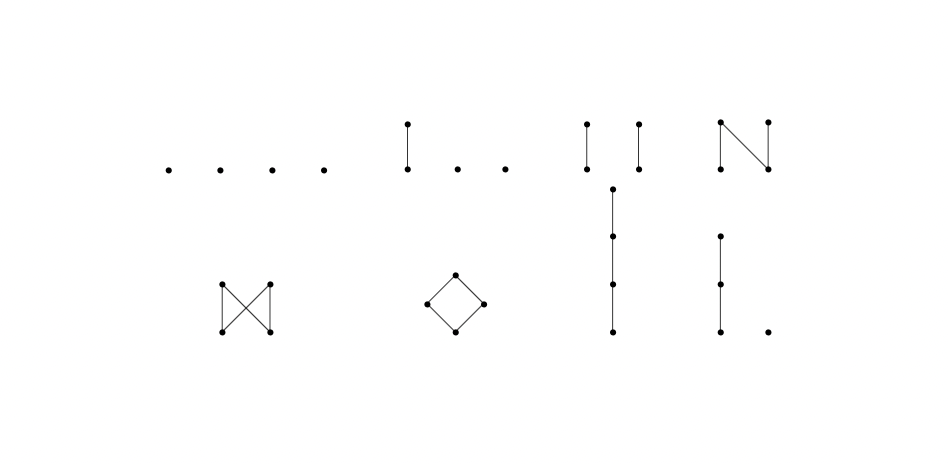
  - 这里是所有含有四个元素的偏序集中的非自对偶偏序集, 共有8个, 显然这些偏序集的对偶都是成对出现的