写在前面
前一篇总结了偏序集以及偏序集上的基本运算, 还有格的一些简单定义与例子, 这次重点讲一下格的其他主要性质以及分配格的一些定理与在组合中的应用.
预备知识
-
若$x,y\in P$, 那么$x,y$的上界为满足$z\geq x,z\geq y$的元素$z\in P$.
-
$x,y$的最小上界为$x,y$的上界$z$, 使得对$x,y$的每一个上界$w$, 都有$w\geq z$.
-
若$x,y$最小上界存在, 则唯一, 记为$x\vee y$(并, 上确界), 同理, 最大下界记为$x\wedge y$(交,下确界).
-
格(lattice): 是一个偏序集$L$, 其中每一对元素的最小上界和最大下界都存在.
- 格满足的一些性质: \(\begin{cases}a.运算\vee,\wedge是结合,交换,幂等的\\b. x\wedge(x\vee y)=x=x\vee(x\wedge y)\\c. x\wedge y=x\iff x\vee y=y\iff x\leq y\end{cases}\)
- 交半格: 如果偏序集$P$的每对元素都有交$\wedge$;
- 并半格: 如果$P$的每对元素都有并($\vee$).
- 设$P$是一个有$\hat{1}$的有限交半格, 则$P$是一个格(对偶地, $P$为具有$\hat0$的并半格, 则$P$为格).
- 完全格: 若$L$的每个子集都有交和并, 完全格含有$\hat0,\hat1$.
半模格(semimodular lattice)
$\bigstar$设$L$为一有限格, 则下面两条件等价:
-
$L$分次, 且$L$的秩函数$\rho$满足:
对$\forall x,y\in L$, 有$\rho(x)+\rho(y)\geq\rho(x\wedge y)+\rho(x\vee y)$.
-
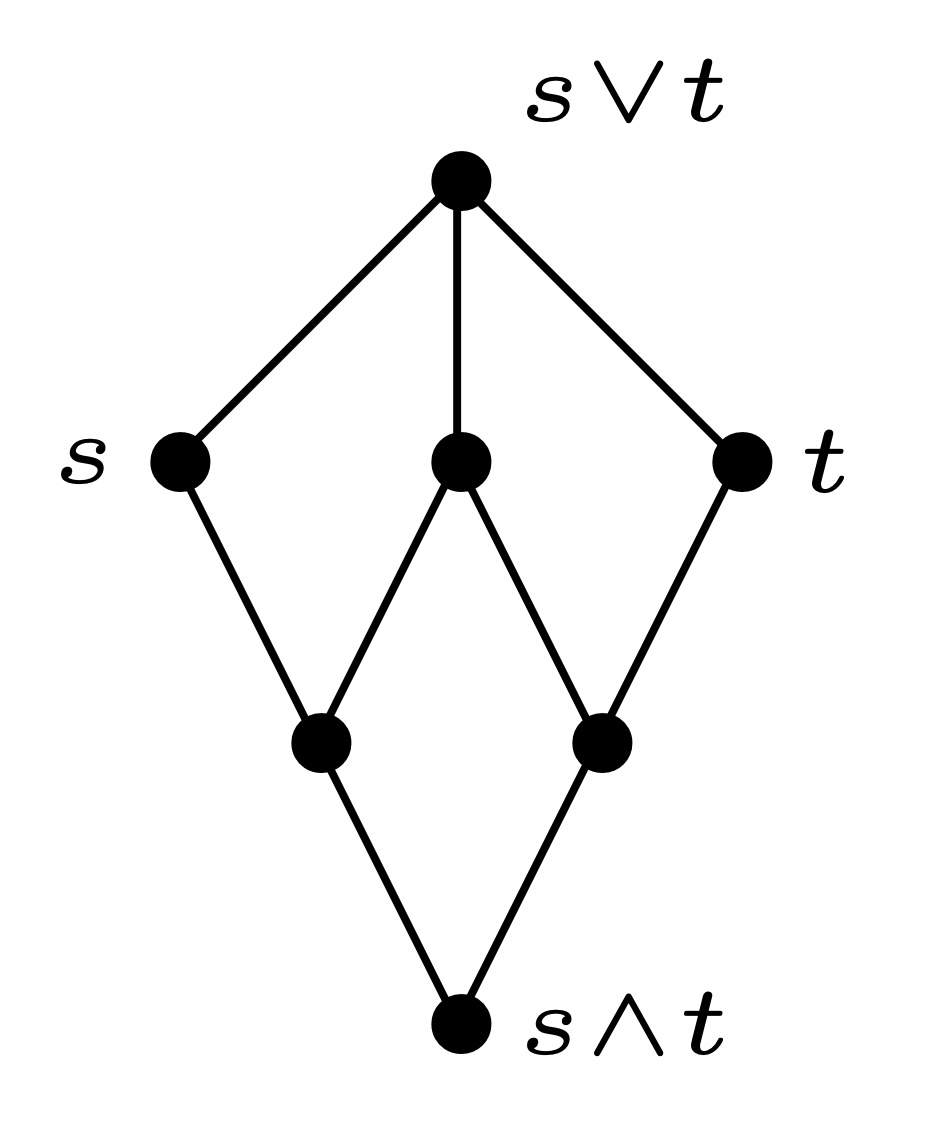
若$x$和$y$都覆盖$x\wedge y$, 则$x\vee y$覆盖$x$和$y$.
$1\Longrightarrow2$:
若$x,y$都覆盖$x\wedge y$, 则显然有$\rho(x)=\rho(y)=\rho(x\wedge y)+1$, 并且有$\rho(x\vee y)>\rho(x)=\rho(y)$. 由 1 中结论, 整理得到:
\[\rho(x)+1=\rho(y)+1\geq\rho(x\vee y)>\rho(x)=\rho(y),\]所以$\rho(x)+1=\rho(y)+1=\rho(x\vee y)$.
$2\Longrightarrow1$:
反证法,取长度最小的非分次区间,找使得极大链长度相同的元素覆盖区间的左端点,由条件 2 推出矛盾.
下面证明不等式
\[\rho(x)+\rho(y)\geq\rho(x\wedge y)+\rho(x\vee y)\]成立.
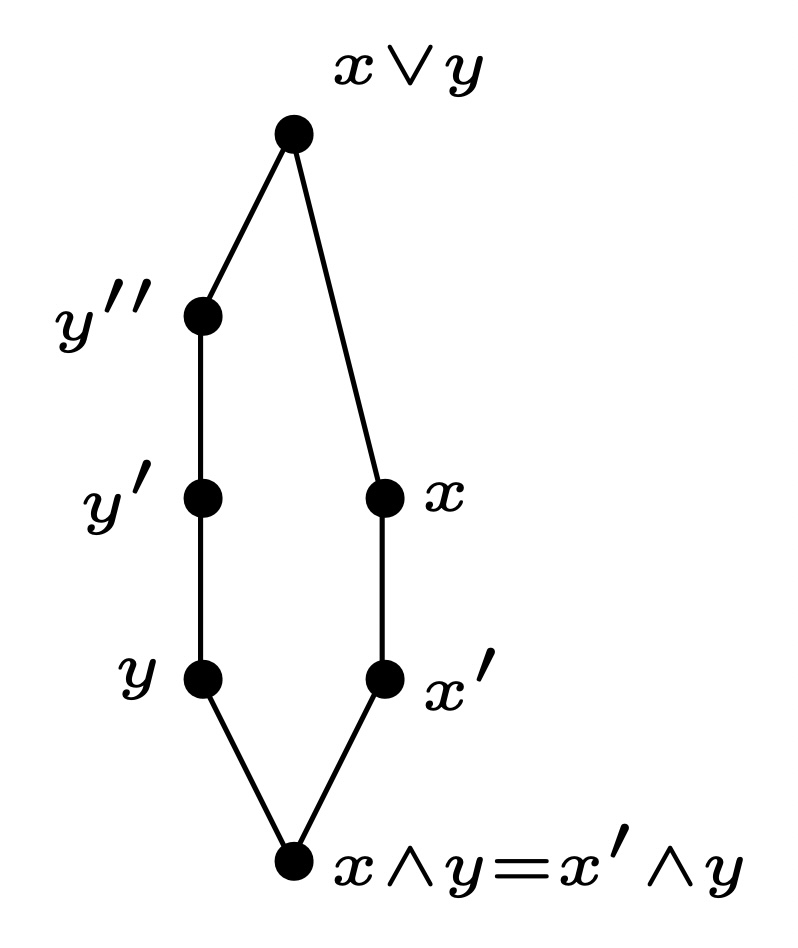
设存在$x,y\in L$, 使得:
\[\rho(x)+\rho(y)<\rho(x\wedge y)+\rho(x\vee y),\]选取$\ell(x\wedge y,x\vee y)$最小, 然后让$\rho(x)+\rho(y)$最小, 假设$x\wedge y<x’<x$(根据条件 2 的逆否命题, 不可能有$x,y$都覆盖$x\wedge y$),可以做出大致的 Hasse 图如下:
由图得到:
\[\rho(x')+\rho(x'\vee y)<\rho(x')+\rho(x\vee y),\]所以$x\wedge y=x’\wedge y$, 代入上面两式
\[\begin{aligned} \rho(x)+\rho(y)&< \rho(x\wedge y)+\rho(x\vee y)\\ &\leq\rho(x')+\rho(y)-\rho(x'\vee y)+\rho(x\vee y) \end{aligned}\]整理得到:
\[\rho(x)+\rho(x'\vee y)< \rho(x')+\rho(x\vee y)\]显然有$x\wedge (x’\vee y)\geq x’$, 并且$x\vee (x’\vee y)=x\vee y$, 令$X=x, Y=x’\vee y$, 我们得到$X,Y\in L$, 满足:
\[\rho(X)+\rho(Y)<\rho(X\vee y)+\rho(X\wedge Y),\\ \ell(X\wedge Y,X\vee Y)<\ell(x\wedge y,x\vee y),\]矛盾.
-
满足上述任何一个条件(命题)的有限格称为
有限上半模格, 或有限半模格. -
在元素为 6 的格中(共有 15 个), 有限半模格有 8 个. 分别是: $\bf6$,包含菱形结构的格 5 个, 以及两个穿过菱形的一条对角线的格两个.
- 存在唯一一个七个元素的不是模格的半模格, 其 Hasse 图如下
-
若有限格$L$的对偶$L^*$为半模格, 称$L$为
下半模格. -
有限格$L$为模格$\iff L$是分次的, 且其秩函数$\rho$满足
\[\rho(x)+\rho(y)=\rho(x\wedge y)+\rho(x\vee y), \quad\forall x,y\in L.\] -
元素个数小于 6 的半模格均为模格.
-
有补: 若格$L$具有$\hat0$和$\hat1$(有限格显然具有$\hat0,\hat1$), 且对于$\forall x\in L$, 均有$y\in L$,使得$x\wedge y=\hat0,x\vee y=\hat1$.
-
唯一有补: 若对于$\forall x\in L$, 互补元$y$唯一.
-
相对有补: 若$L$的每一个区间$[x,y]$自身有补.
-
原子: 覆盖$\hat0$的元素, 如果$L$每一个元素都是一些原子的并, 则称$L$是原子的(或: 点格 point lattice).
- 上原子: 被$\hat1$覆盖的元素, 上原子格同理.
$\bigstar$设$L$为一个有限半模格, 下面两条件等价:
- $L$相对有补;
- $L$是原子的.
满足上述 1 或 2 条件的有限半模格称为有限几何格.
分配格(distributive Lattices)
通过分配律定义的格,
- $x\vee (y\wedge z)=(x\vee y)\wedge(x\vee z)$.
- $x\wedge (y\vee z)=(x\wedge y)\vee(x\wedge z)$.
两者可以互相转换.
- 所有的分配格都是模格.
- 偏序集$P$的序理想构成的格$J(P)$;(序理想的并和交仍为序理想)
$\bigstar$定理: (有限分配格基本定理,FTFDL) 设$L$是有限分配格, 则(在同构意义下)存在唯一的有限偏序集, 使得$L\cong J(P)$.
- 并运算不可约: $\forall x\in L$,如果$x$不能写成$x=y\vee z$的形式, 其中$y<x,z<x$.
- 规定$\hat0$不是并运算不可约的.
- 交运算不可约: $\forall x\in L$,如果$x$不能写成$x=y\wedge z$的形式, 其中$y>x,z>x$.
-
有限偏序集$P$中的序理想$I$在$J(P)$中是并运算不可约的$\iff I$是$P$的主理想;
命题 2:$J(P)$中并运算不可约元所成集合作为$J(P)$的(诱导)子偏序集, 与$P$同构, 即$J(P)\cong J(Q)\iff P\cong Q$.
证明 FTFDL:(构造双射证明)
通过上述命题, 欲证明$L\cong J(P)$, 只需证明$P$是$L$上的并运算不可约元构成的子偏序集即可.
取$x\in L$, 令$I_x={y\in P:y\leq x}$, 显然有$I_x\in J(P)$, 定义映射:
\[\begin{aligned} \phi:L&\to J(P)\\ x&\mapsto I_x=\{y\in P:y\leq x\} \end{aligned}\]该映射为一保持交运算的单射, 且其逆也保序. 只需证明$\phi$满射即可.
令$I\in J(P), x=\bigvee{y:y\in I}$, 只需证明$I=I_x$.(陪集等于像集)包含关系$I\subseteq I_x$显然成立($J(P)$定义,序理想), 设$z\in I_x$, 有
\[\bigvee\{y:y\in I\}=\bigvee\{y:y\in I_x\},\]上式两边取交, 即$\wedge z$, 应用分配律, 得到
\[\bigvee\{y:y\wedge z\in I\}=\bigvee\{y:y\wedge z\in I_x\},\]我们有$\bigvee{y:y\wedge z\in I_x}=z$, 因为$z$并运算不可约, 存在$y\in I$, 使得$y\wedge z=z\iff z\leq y$.
由于$I$为序理想, 所以$z\in I$, $I_x\subseteq I$, $I_x=I$.
-
有限性的分配格: 具有$\hat0$的局部有限分配格$L$;因此$L$有唯一的秩函数$\rho:L\to\mathbb{N}$,其中$\rho(x)$等于任意一条从$\hat0$到$x$的饱和链的长度.
-
$\forall i\in \mathbb{N}$, $L$有$p_i$个秩为$i$的元素, $p_i<\infty$,定义秩生成函数$F(L,q)$:(可能是幂级数) \(F(L,q)=\sum_{i\geq0}p_iq^i.\)
命题 3: 设$P$是一个所有主序理想都有限的偏序集, 则$P$的所有有限序理想按照包含关系排序构成的偏序集$J_f(P)$是有限性的分配格. 反之,如果$L$是一个有限性的分配格, $P$是它的并运算不可约元构成的子偏序集, 则$P$的每一个主序理想都是有限的且有$L=J_f(P)$.
| 命题 4: 如果$P$是一个$n$元偏序集, 那么$J(P)$是分次的且秩为$n$, 进一步, 作为$P$的序理想, 元素$I\in J(P)$是秩$\rho(I)$就是$I$的元素个数$ | I | $. |
例子:
-
$P={\bf n},J(P)\cong\bf n+1$;
-
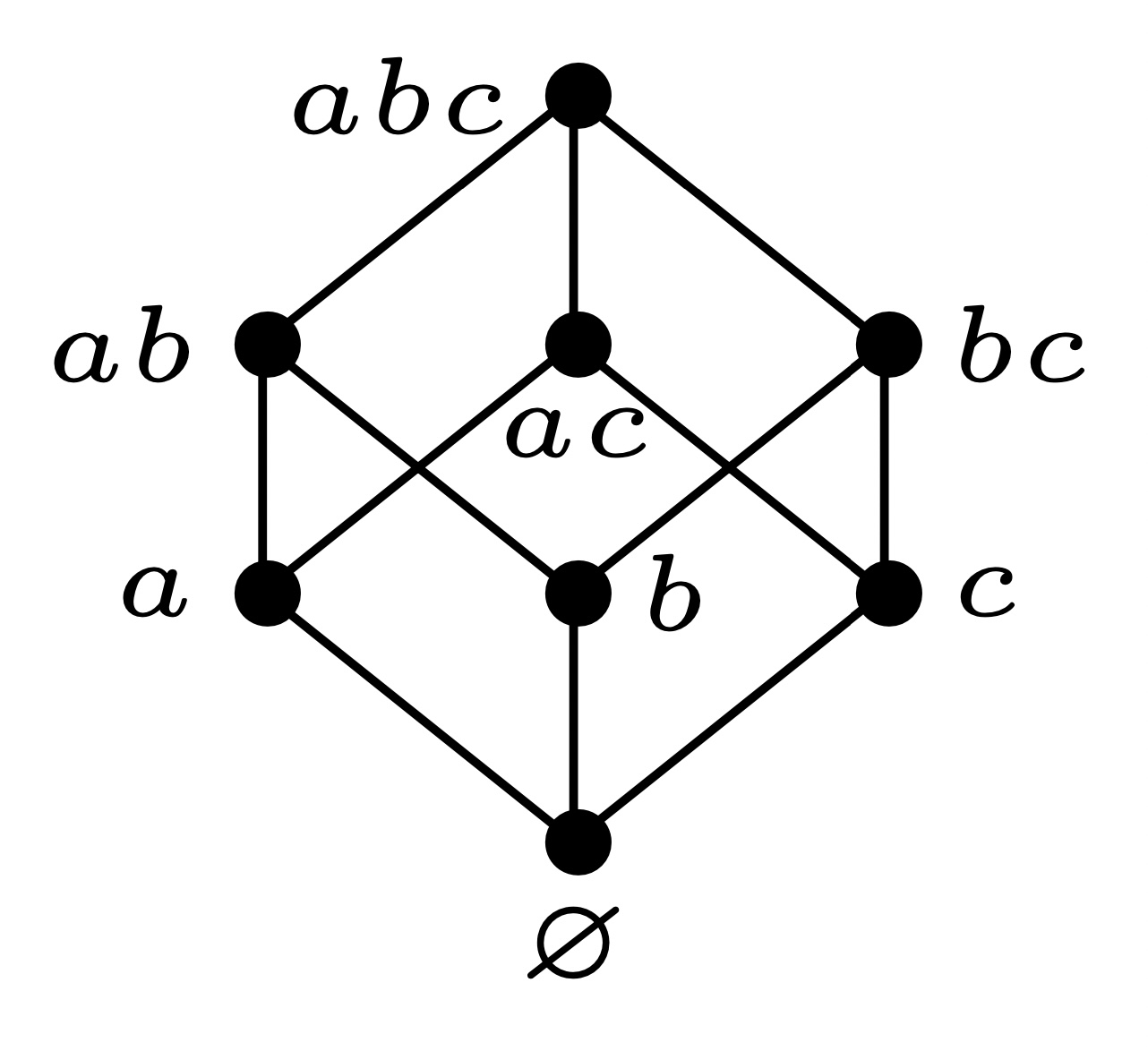
$P=n{\bf 1},J(n{\bf1})=B_n$, 其中$B_n$:
$n\in \mathbb{N}$, $[n]$的所有子集的集合$2^{[n]}$构成偏序集$B_n$, 称为子集格.
称$B_n$为一个秩为$n$的布尔代数.
绘制$J(P)$的 Hasse 图的方法:
-
找出$P$的极小元所成集合$I$, $ I =m$. 绘制$B_m\cong J(I)$. - 选$P-I$的极小元$x$, 在$J(I)$上添加一个并运算不可约元, 该元素覆盖$\Lambda_x-{x}$,($\Lambda_x$为主序理想) 并且满足覆盖条件的元素的并构成一个布尔代数.绘制所有的新的必要的并元素.
- 重复 2,使得对每一个元素, 其覆盖都有并, 得到分配格$J(I\cup {x})$.
- 选择$J-I-{x}$的极小元$y$, 在$J(I\cup {x})$上加上并运算不可约元, 覆盖序理想$\Lambda_{y}-{y}$.
- 接着绘制, 填满所有的覆盖, 得到$J(I\cup{x,y})$,继续这一过程得到$J(P)$.
例子:
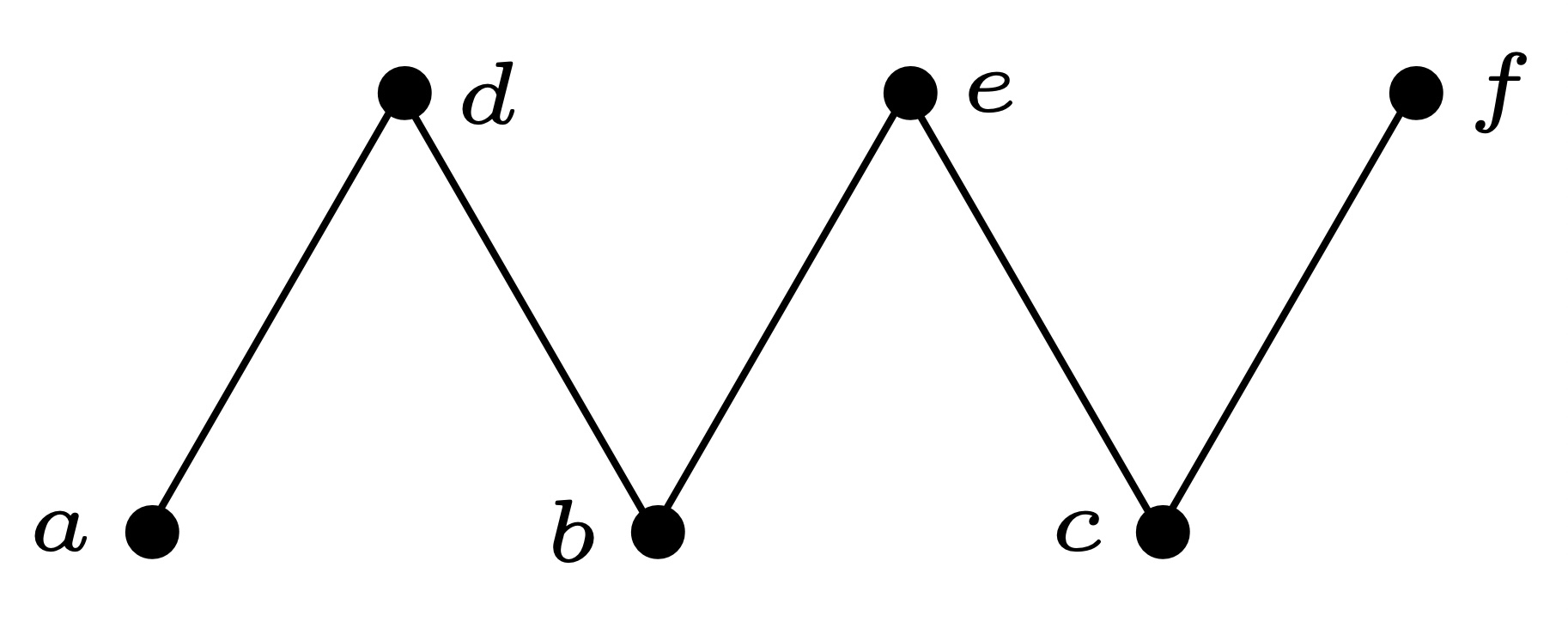
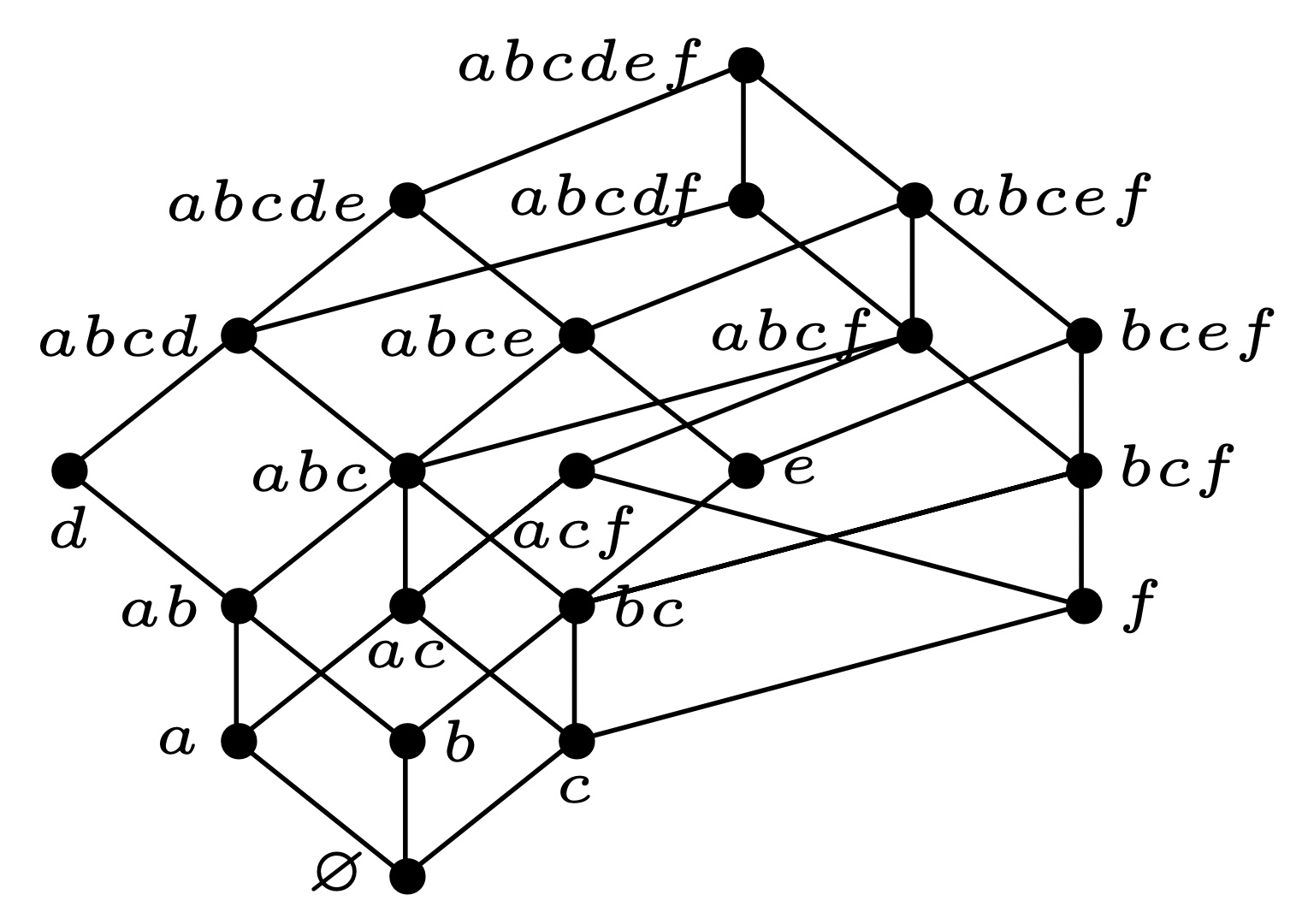
对于栅格(fences)$P={a,b,c,d,e,f}$, 其 Hasse 图如下:
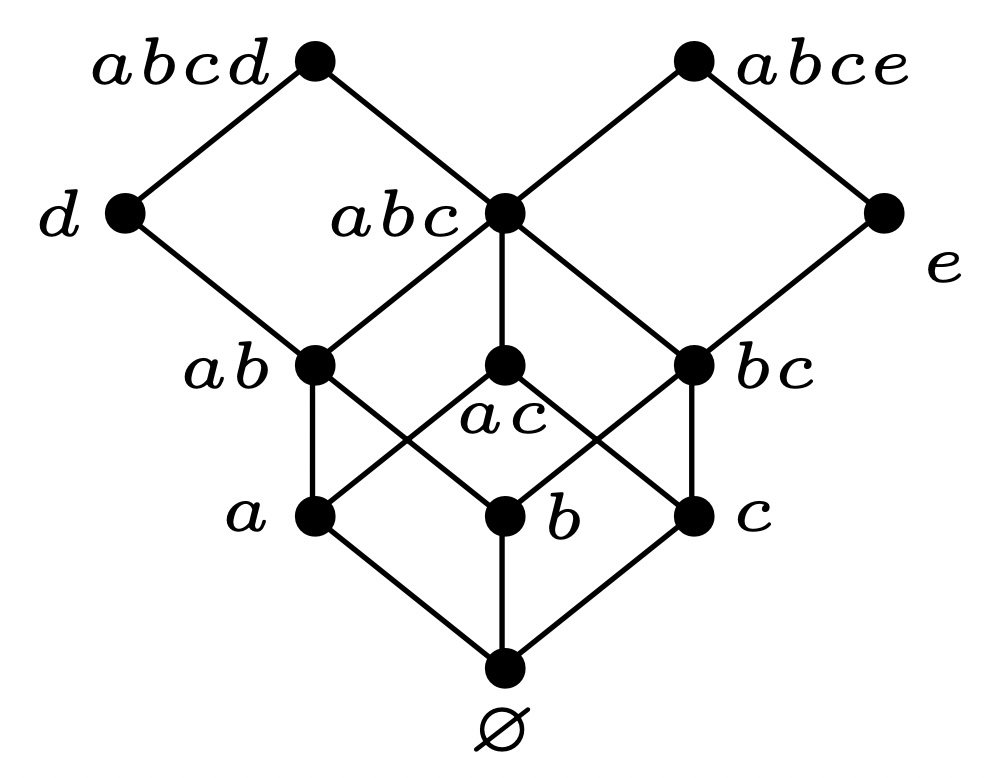
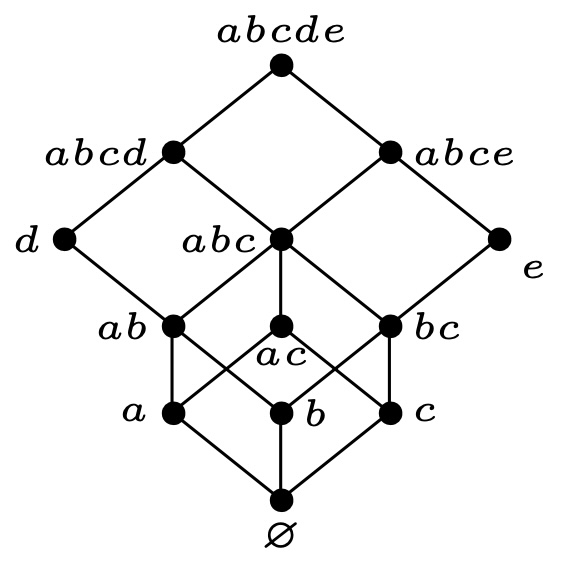
- 先绘制极小元构成的集合$I={a,b,c}$的序理想构成的格$J(I)$. 如下图所示
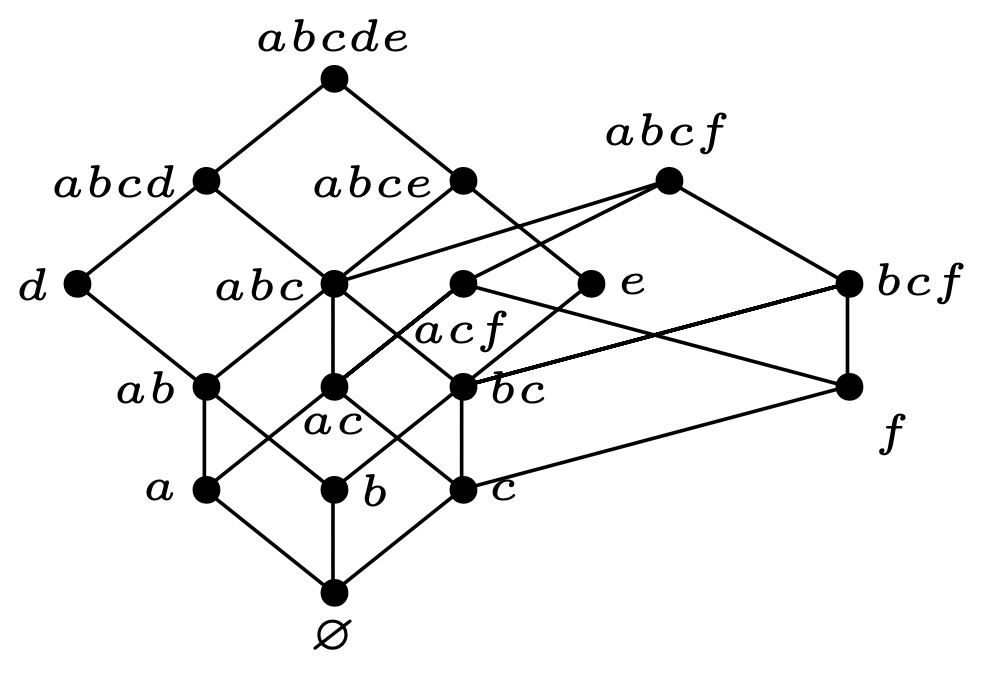
寻找去掉极小元之后的偏序集$P-I$的极小元${d}$, 绘制并连接:
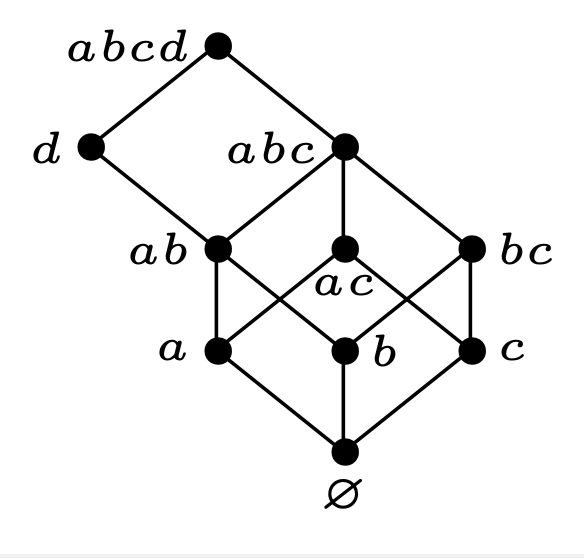
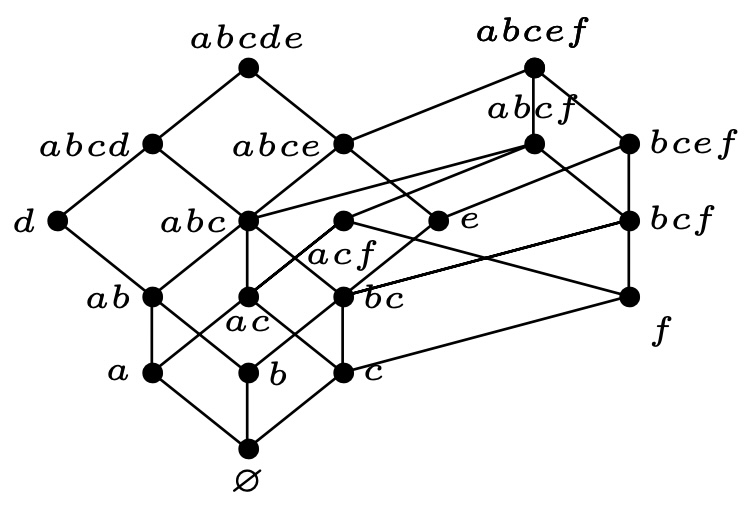
同理, 分别添加${e},{f}$, 并将有覆盖关系的边进行连接如下:
- 最后可以得到下面的 Hasse 图, 即为$J(P)$.
从图中直接可以得到: (用颜色区分不同的秩)
\(F(J(P),q)=1+3q+4q^2 +5q^3 +4q^4 +3q^5 +q^6\)