写在前面
这一部分主要是计数组合学中的第 3.5 的内容.
分配格的简单性质
容易验证:
- $P$ 的$k$元序理想的个数等于$J(P)$中秩为$k$的元素个数.
- $P$ 中$k$元反链$(k≥1)$ 的个数等于 $J(P)$ 中恰好覆盖 $k$ 个元素的元素个数
命题 1
设 $P$ 为有限偏序集并且 $m ∈ \mathbb N$, 则下面的数目相等:
- 保序映射$σ:P→\bf m$的个数,
- $J(P)$ 中长为 $m$ 的可重链 $\hat0=I_0 ≤I_1 ≤···≤I_m =\hat1$ 的条数,
- $J(P×{\bf m−1})$中元素的个数.
证明: (构造双射)
$σ:P→\bf m$,(偏序集$P$到$m$元链的映射) 定义$I_j=\sigma^{-1}({\bf j})$, 给定$\hat0=I_0 ≤I_1 ≤···≤I_m =\hat1$, 定义$J(P×{\bf m−1})$的序理想为
\[I=\{(x,y)\in P\times \textbf{m−1}:\ x\in I_{m-j} \},\]定义上述的$\sigma$为: 如果存在$j$使得$(x,j)\in I$, 则$\sigma(x)=\min{m-j:\ (x,j)\in I}$, 若不存在, 则$\sigma(x)=m$. 这构成了满足上条件的双射. 或者直接由$1,3$得到:
\[{\mathbf m}^P\cong({\bf 2^{m-1}})^P\cong {\bf2}^{\mathbf{m-1}\times P}.\]
命题 2
设 $P$ 为有限偏序集并且 $m ∈ \mathbb N$, 则下面的数目相等:
- 保序满射$σ:P→\bf m$的个数,
- $J(P)$ 中长为 $m$ 的链 $\hat0=I_0 <I_1 <···<I_m =\hat1$ 的条数.
-
$P$到全序的扩张($P$的线性扩张): 如果$ P =n$,则保序双射 $\sigma:P\to {\bf n}$. - 扩张个数记为$e(P)$,显然等于$J(P)$中极大链的条数.
分配格与格路计数
可以将$P$到全序的扩张$\sigma:P\to\bf n$等同于$P$中元素的排列: $\sigma^{-1}(1),…,\sigma^{-1}(n)$, 或者将$J(P)$的极大链等同于下面欧式空间中的”格路”.
| 假设$C_1,C_2,\cdots,C_k$为$P$的一个链划分, (Dilworth 定理推论指出$k$的最小可能值为$P$的反链的最大基数), 定义映射$\delta:\ J(P)\to \mathbb{N}^k$ ,$\delta(I)=( | I\cap C_1 | , | I\cap C_2 | ,\cdots, | I\cap C_k | )$. |
| 赋予$\mathbb{N}^k$乘积序, 则$\delta$为一个单的格同态, 且保持覆盖关系, ($J(P)$同构于$\mathbb{N}^k$)的一个子格, 如果选择每一个$ | C_i | =1$, 得到一个保秩的单的格同态$J(P)\to B_n$, 区中$ | P | =n$.) |
给定$\delta:\ J(P)\to \mathbb{N}^k$, 定义$\Gamma_\delta=\bigcup_T cx(\delta(T))$, 其中$cx$表示$\mathbb{R}^k$中的凸包而$T$取遍$J(P)$中同构于布尔代数的区间. $\Gamma_\delta$是$\mathbb{R}^k$的一个紧多面体子集.
$J(P)$中最长链的数目等于在$\Gamma_\delta$中从原点$(0,0,…,0)=\delta(\hat0)$到$\delta(\hat1)$的格路的条数, 每步沿着坐标轴方向移动一个单位.
即, 扩张个数$e(P)$等于将$\delta(\hat1)$表示为$\delta(\hat1)=v_1+v_2+\cdots+v_n$的方法数, 其中每一个$v_i$是在$\mathbb R^k$中的一个单位向量, 并且对所有的$i$, 有$\sum_{k=1}^iv_k\in \Gamma_\delta$.
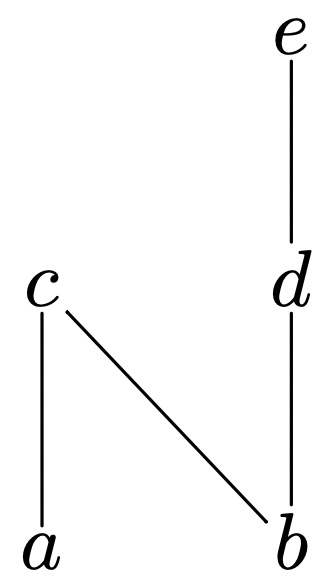
例 1:(不交并)具体问题
对于下面的偏序集, 取$C_1={a,c}, C_2={b,d,e}$.
利用前面一小节的方法, 可以容易的找出$J(P)$, 如下图所示, 进行了元素的标记:
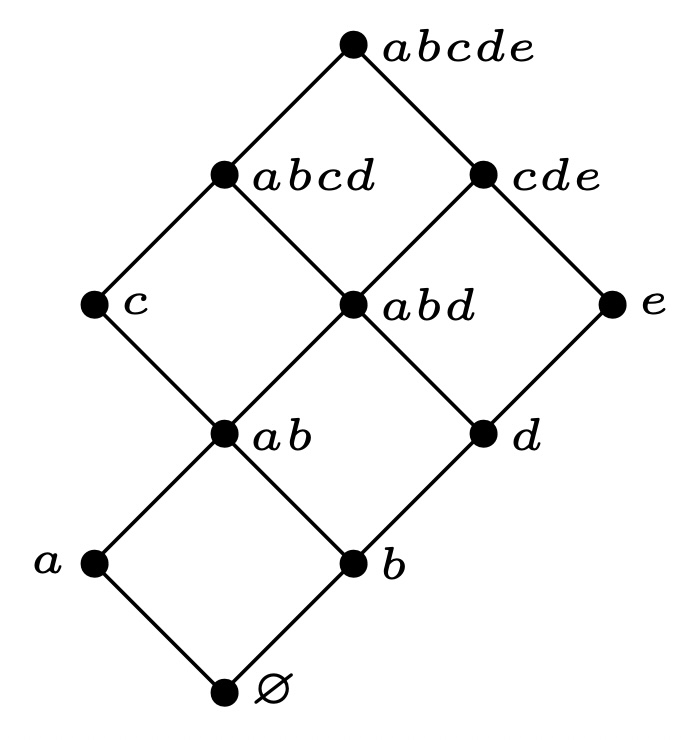
通过上面的坐标标记, 可以得到:
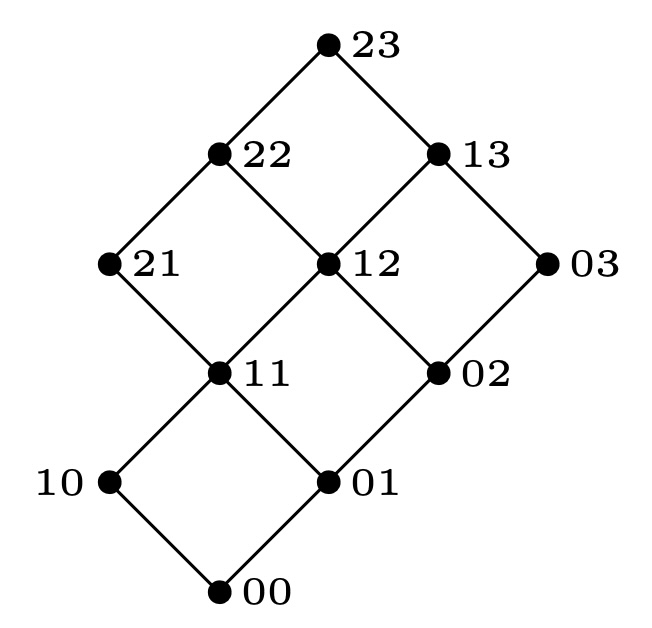
从图中的$\varnothing$到$abcde$, 即从$(0,0)$到$(2,3)$,有$9$条可以选择的路, 所以$e(P)=9$.
例 2:(不交并)一般的例子
| 设$P=C_1+C_2$, 且$ | C_1 | =m, | C_2 | =n$, 则$\Gamma_\delta$为一个$m\times n$长方形网格, 于是$e(P)=\binom{m+n}n$, 从线性序扩张角度, 构造$\sigma:\ P\to \bf m+n$, 完全由$\sigma(C_1)$确定, 为$\bf m+n$ 的任意$m$元子集, 由此也可以得到$e(P)=\binom{m+n}m$. |
推广:
\[e(P)=\binom{n_1+\cdots+n_k}{n_1,\cdots,n_k}e(P_1)\cdots e(P_k).\]
如果$P=P_1+\cdots+P_k,n_i= P_i $, 则
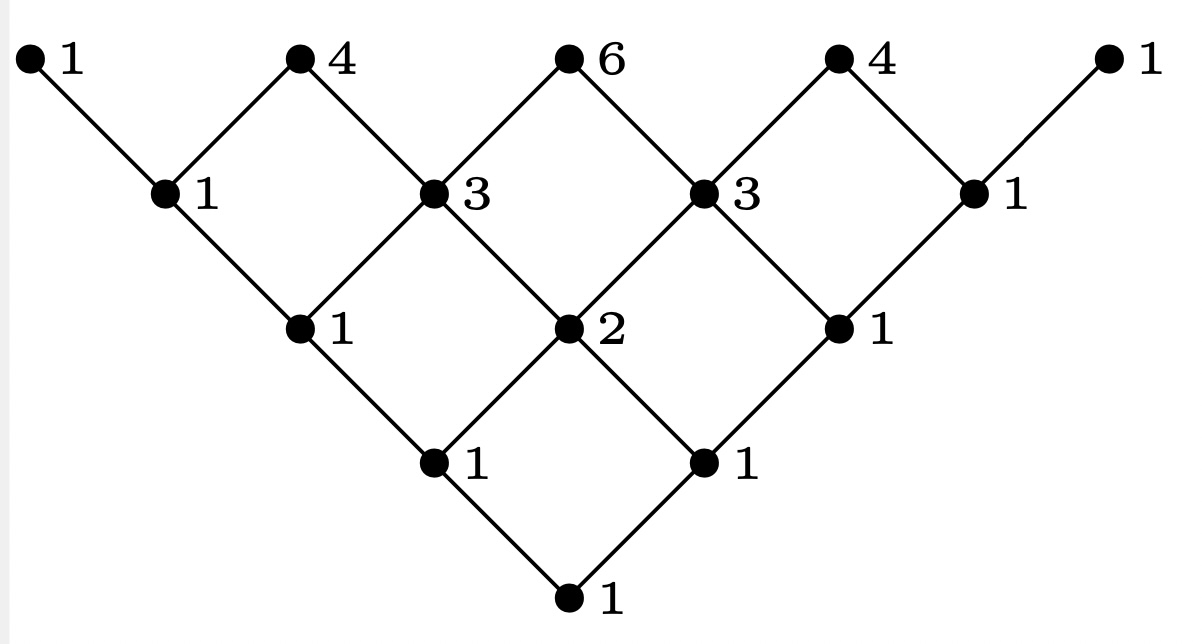
例 3: (笛卡尔积)
设$P=\bf 2\times n$, 取$C_1={(2,j):\ j\in \bf n}$, $C_2={(1,j):\ j\in\bf n}$, 则$\delta(J(P))={(i,j)\in\mathbb{N}^2:\ 0\leq i\leq j \leq n}$. 当$n=3$, 即$P=\bf 2\times 3$, 偏序集$P$如下所示:
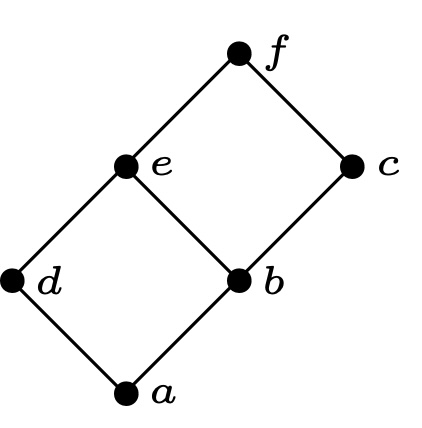
容易得到$J(P)$如下图:
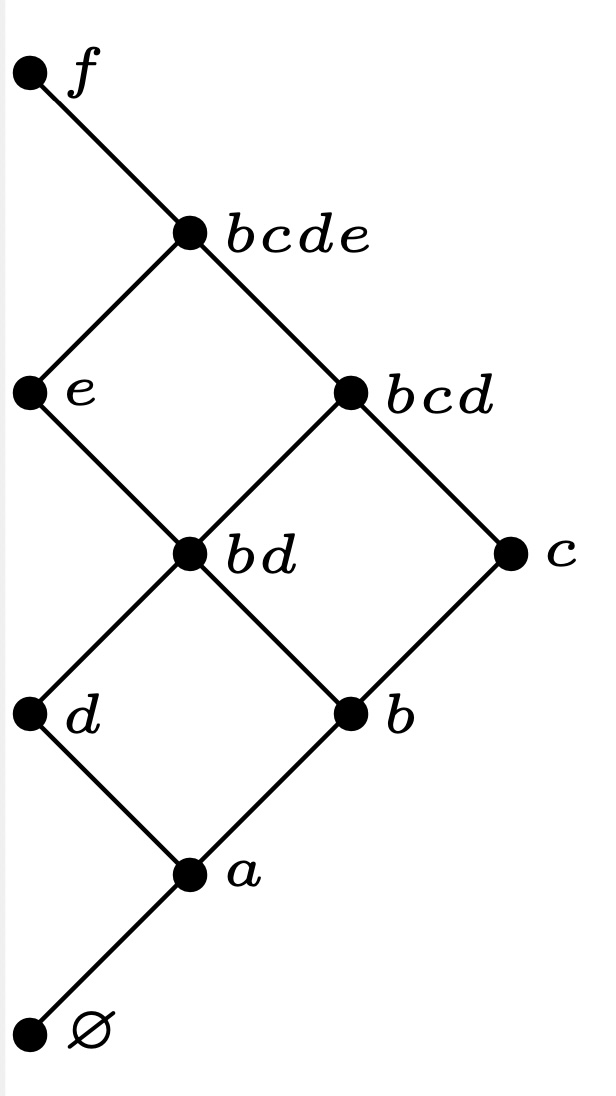
这等价于不穿过$y=x$且只往上和右走一个格的格路数, 显然图中为$5$. 一般地, $e(2\times {\bf n})=\frac1{n+1}\binom {2n}n$.
递推关系
将$e$看作$J(P)$上的函数, 即如果$I\in J(P)$, 则$e(I)$表示$I$作为$P$的偏序子集扩张到全序集的个数, 因此$e(I)$等于在$J(P)$中从$\hat0$到$I$ 的饱和链的条数. 于是
\[e(I)=\sum_{I'}e(I'),\]其中$I’$取遍$J(P)$中$I$所覆盖的所有元素, 类似于杨辉三角, $e(I)$就是恰好在$I$下面的$e(I’)$的和.
一个简单的例子就是$P=\mathbb{N+N}$, 记$J_f(P)$为$P$的有限序理想构成的格, 则有$J_f(P)\cong \mathbb{N\times N}$.