写在前面
前面铺垫了很多偏序集和格,分配格等的基本知识, 下面开始以这些代数结构为研究对象, 探寻其上的一些性质与关系, 我们先以关联代数的定义开始说起.
关联代数简介
定义
- 令$\mathrm{Int}(P)$表示$P$上所有的区间的集合, (空集不是区间)
- 令$K$为一个域, 定义$f:{\rm Int}(P)\to K$, 用$f(x,y)$表示$f([x,y])$.
$P$在$K$上的关联代数$I(P,K)$定义为: 由所有的函数$f:{\rm Int}(P)\to K$构成的$K$-代数, 其中乘法(卷积)定义为:
\[(fg)(x,y)=\sum_{x\leq {\Large{}_{\stackrel{\!\,{}_z}{\,\!{}^\cdot}}}\leq y}f(x,z)g(z, y).\]且关联代数$I(P,K)$有双侧单位元的结合$K$-代数, 单位元记为$\delta$或者$1$,定义为
\[\delta(x,y)= \begin{cases} 1, & \mbox{if}\ x=y,\\ 0, & \mbox{if}\ x\ne y. \end{cases}\]取数域$K=\mathbb C$即可, 可将$I(P,\mathbb C)$简记为$I(P)$.
另一种表达:
将$I(P,K)$视为由所有的形式表达式:
\[f=\sum_{[x,y]\in \mathrm{Int}(P)}f(x,y)[x,y]\]组成的, 其中卷积定义如下:
\[[x,y]\cdot[z,w]=\begin{cases} [x,w],&\mbox{if }y=z,\\[5pt] 0,&\mbox{if } y\ne z, \end{cases}\]并且通过双线性(允许$[x,y]$的无限线性组合)扩展到所有的$I(P,K)$.
有限情形的例子
如果$P$有限, 其中元素记为$x_1,\cdots,x_n$, 其中$x_i<x_j\Rightarrow i<j$, 于是$I(P)$同构于$\mathbb C$上满足: 若$x_i\not\leq x_j$则$m_{ij}=0$的上三角矩阵$M=(m_{ij}),\ 1\le i,j\le n$构成的代数. (可以从$m_{ij}$到$f(x_i,x_j)$建立映射关系)
如果$P$由下图给出, 则$I(P)$同构于形式为
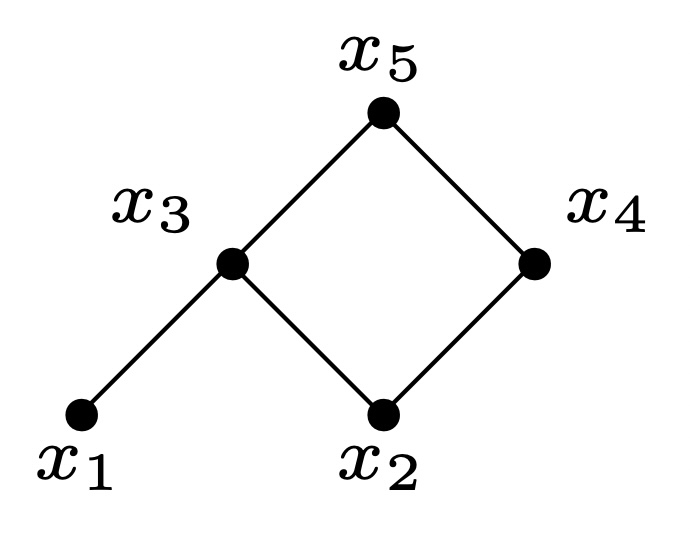 \(\begin{bmatrix}
∗ & 0 & ∗ & 0 & ∗\\
0 & ∗ & ∗ & ∗ & ∗\\
0 & 0 & ∗ & 0 & ∗\\
0 & 0 & 0 & ∗ & ∗\\
0 & 0 & 0 & 0 & ∗\\
\end{bmatrix}\)
的矩阵构成的代数.
\(\begin{bmatrix}
∗ & 0 & ∗ & 0 & ∗\\
0 & ∗ & ∗ & ∗ & ∗\\
0 & 0 & ∗ & 0 & ∗\\
0 & 0 & 0 & ∗ & ∗\\
0 & 0 & 0 & 0 & ∗\\
\end{bmatrix}\)
的矩阵构成的代数.
性质
设$f\in I(P)$, 则下面的条件等价:
- $f$有一个左逆元;
- $f$有一个右逆元;
- $f$有一个双侧逆元(必然是唯一的左逆元和右逆元);
- $f(x,x)\ne0,\ \forall x\in P$成立.
进一步, 如果$f^{-1}$存在, 则$f^{-1}(x,y)$仅取决于偏序集$[x,y]$.
证明:
设$fg=\delta$, 等价于$\forall x\in P$, 有$f(x,x)g(x,x)=1$, $\forall x,y\in P$, 且满足$x<y$, 有
\[g(x,y)=-f(x,x)^{-1}{\large\sum}\limits_{x<z\le y}f(x,z)g(z,y),\tag{1}\]于是$f$有右逆元$g\iff \forall x\in P, f(x,x)\ne0$, 并且此时$f^{-1}(x,y)$仅取决于$[x,y]$.
同理, 设$hf=\delta$, 即得到$f$有右逆元$\iff\forall x\in P, f(x,x)\ne0\iff f$有右逆元.
另外, 由$fg=\delta,hf=\delta$, 得到$g=h$.
关联代数中有用的函数
zeta函数
$\zeta(x,y)=1,\forall x,y\in P, x\le y$. 所以有
\[\begin{aligned} \zeta^2(x,y)&=\sum_{x\le z\le y}1=\mbox{card}[x,y],\\[5pt] \zeta^k(x,y)&=\sum_{x=x_0\le x_1\le\cdots \le x_k= y}1, \end{aligned}\]即从$x$到$y$的长度为$k$的可重链的条数. 类似有
\[(\zeta-1)(x,y)=\begin{cases} 1,&x<y,\\ 0,&x=y. \end{cases}\]于是$(\zeta-1)^k(x,y)$是从$x$到$y$的长度为$k$的链$x=x_0< x_1<\cdots < x_k= y$的条数.
下面是$(2-\zeta)(x,y)\in I(P)$,
\[(2-\zeta)(x,y)=\begin{cases} 1,&x=y,\\ -1,&x<y. \end{cases}\]Möbius反演
由上述讨论, 局部有限偏序集$P$的zeta函数$\zeta$可逆, 其逆称为$P$的Möbius函数, 记为$\mu$(或者$\mu_P$). 通过归纳定义, 可得到:
\[\hspace{-20em}\mu\zeta=\delta\iff\\[5pt] \begin{cases} \mu(x,x)=1,\quad\forall x\in P, \\[5pt] \mu(x,y)=-\sum_\limits{x\le z<y}\mu(x,z),\ \forall x<y\in P, \end{cases}\]第二个式子可以直接通过$(1)$式代入后展开得到.
Möbius反演公式
设$P$为所有主序理想有限的偏序集, 令$f,g: P\to\mathbb C$, 有
\[g(x)=\sum_{y\le x}f(y),\quad\forall x\in P,\tag2\]当且仅当
\[f(x)=\sum_{y\le x}g(y)\mu(y,x),\quad \forall x\in P.\]这个证明看原版英文书中有一个通过平凡计算证明的方法, 感觉要更好理解一些.(子空间作用有点抽象) 假定$(2)$成立, 则有
\[\begin{aligned} \sum_{y\le x}g(y)\mu(y,x)&=\sum_{y\le x}\mu(y,x)\sum_{z\le y}f(z)\\ &=\sum_{z\le x}f(z)\sum_{z\le y \le x}\mu(y,x)\\ &=\sum_{z \le x}f(z)\delta(z,x)=f(x) \end{aligned}\]其中倒数第二个等号成立是因为:
\[\delta(z,x)=(\zeta\mu)(z,x)=\sum_{z\le y\le x}\zeta(z,y)\mu(y,x)=\sum_{z\le y\le x}\mu(y,x)\]对偶形式
设$P$为一个所有主对偶序理想$V_x$均有限的偏序集, 令$f,g\in \mathbb C^P$, 则有
\[g(x)=\sum_{y\ge x}f(y),\quad \forall x\in P,\]当且仅当
\[f(x)=\sum_{y\ge x}\mu(x,y)g(y), \quad \forall x\in P.\]一个例子: Möbius反演公式的意义
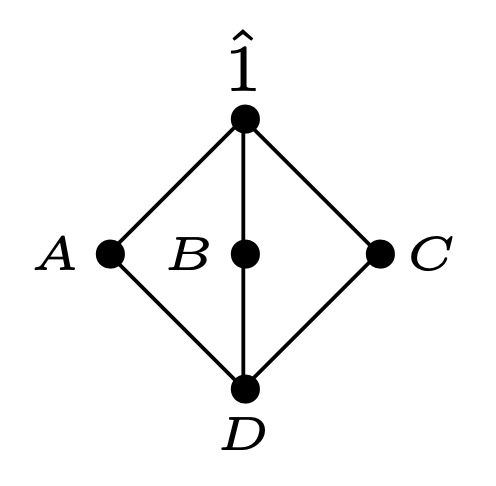
回忆本章开头的一个例子: 有限集合$A,B,C,D$, 满足:
\[D=A\cap B=A\cap C=B\cap C=A\cap B\cap C,\]通过容斥原理得到:
\[\begin{aligned} |A\cup B\cup C|&=|A|+|B|+|C|-|A\cap B|-|A\cap C|-|B\cap C|+|A\cap B\cap C|\\ &=|A|+|B|+|C|-2|D| \end{aligned}\]下面通过Möbius反演解释上述等式:
给定$n$个有限集合$S_1,…,S_n$, 令$P$为它们所有的交集在包含关系下构成的偏序集, 其中包括空交$S_1\cup\cdots\cup S_n=\hat1$, 若$T\in P$, 令$f(T)$表示$P$中属于$T$但不属于任何$T’<T$的元素的个数, 令$g(T)= T $.
下面通过上述的反演公式找出关于
\[|S_1\cup\cdots\cup S_n|=\sum_{T\le \hat1}f(T)=g(\hat1),\]的表达式, 已知:
\[g(T)=\sum_{T'\le T}f(T'),\]由$P$上的Möbius反演得到
\[\begin{aligned} 0=f(\hat1)&=\sum_{T\in P}g(T)\mu(T,\hat1)\\ &=\sum_{T\le \hat1}g(T)\mu(T,\hat1)\\ &=g(\hat1)\mu(\hat1,\hat1)+\sum_{T< \hat1}|T|\mu(T,\hat1)\\ \Rightarrow g(\hat1)&=-\sum_{T<\hat1}|T|\mu(T,\hat1). \end{aligned}\]于是, 上面的例子就可以直接由反演公式给出(Hasse图如下), 其中
\[\begin{aligned} 0&=\delta(A,\hat1)=(\mu\zeta)(A,\hat1)\\ &=\sum_{A\le z\le \hat1}\mu(A,z)\zeta(z,\hat1)\\ &=\mu(A,A)\zeta(A,\hat1)+\mu(A,\hat1)\zeta(\hat1,\hat1)=1+\mu(A,\hat1)\\[5pt] \Rightarrow& \mu(A,\hat1)=\mu(B,\hat1)=\mu(C,\hat1)=-1 \end{aligned}\] \[\begin{aligned} 0&=\delta(D,\hat1)=(\mu\zeta)(D,\hat1)\\ &=\sum_{D\le z\le \hat1}\mu(D,z)\zeta(z,\hat1)\\ &=\mu(D,D)\zeta(D,\hat1)+\mu(D,A)\zeta(A,\hat1)+\mu(D,B)\zeta(B,\hat1)\\ &+\mu(D,C)\zeta(C,\hat1)+\mu(D,\hat1)\zeta(\hat1,\hat1)\\ &=1+(-3)+\mu(D,\hat1)\\[5pt] \Rightarrow& \mu(D,\hat1)=2 \end{aligned}\]